Page 141 - DMTH201_Basic Mathematics-1

Basic Mathematics – I

Notes By slope-intercept form formula (1) above, equation of the given line is y 3 = 4 (x + 2) or
4x + y + 5 = 0, which is the required equation.

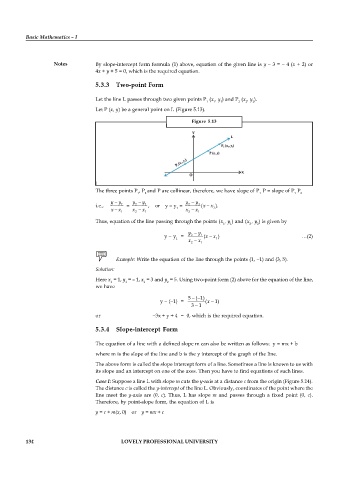
5.3.3 Two-point Form

Let the line L passes through two given points P (x , y ) and P (x , y ).
1 1 1 2 2 2
Let P (x, y) be a general point on L (Figure 5.13).
Figure 5.13

The three points P , P and P are collinear, therefore, we have slope of P P = slope of P P
1 2 1 1 2
y y y y y y
i.e., 1 = 2 1 , or y y = 2 1 (x x 1 ).
x x 1 x 2 x 1 1 x 2 x 1
Thus, equation of the line passing through the points (x , y ) and (x , y ) is given by
1 1 2 2
y y
y y = 2 1 (x x ) …(2)
1 1
x x
2 1
Example: Write the equation of the line through the points (1, 1) and (3, 5).

Solution:
Here x = 1, y = – 1, x = 3 and y = 5. Using two-point form (2) above for the equation of the line,
1 1 2 2
we have
5 ( 1)
y ( 1) = (x 1)
3 1
or 3x + y + 4 = 0, which is the required equation.

5.3.4 Slope-intercept Form

The equation of a line with a defined slope m can also be written as follows: y = mx + b
where m is the slope of the line and b is the y intercept of the graph of the line.
The above form is called the slope intercept form of a line. Sometimes a line is known to us with
its slope and an intercept on one of the axes. Then you have to find equations of such lines.
Case I: Suppose a line L with slope m cuts the y-axis at a distance c from the origin (Figure 5.14).
The distance c is called the y-intercept of the line L. Obviously, coordinates of the point where the
line meet the y-axis are (0, c). Thus, L has slope m and passes through a fixed point (0, c).
Therefore, by point-slope form, the equation of L is
y = c + m(x, 0) or y = mx + c

134 LOVELY PROFESSIONAL UNIVERSITY