Page 167 - DMTH201_Basic Mathematics-1
P. 167
Basic Mathematics – I
Notes
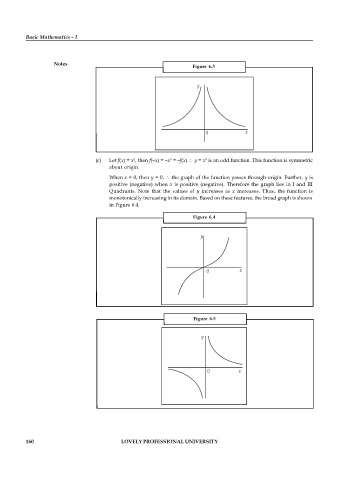
Figure 6.3
0
3
2
3
(c) Let f(x) = x , then f(–x) = –x = –f(x) y = x is an odd function. This function is symmetric
about origin.
When x = 0, then y = 0, the graph of the function passes through origin. Further, y is
positive (negative) when x is positive (negative). Therefore the graph lies in I and III
Quadrants. Note that the values of y increases as x increases. Thus, the function is
monotonically increasing in its domain. Based on these features, the broad graph is shown
in Figure 6.4.
Figure 6.4
0
Figure 6.5
0
160 LOVELY PROFESSIONAL UNIVERSITY