Page 168 - DMTH201_Basic Mathematics-1
P. 168
Unit 6: Functions
Notes
1 1 1
x
(d) Let ( )f x , then (f ) x f ( ) y is an odd function and symmetric
x x x
about origin.
This, function is not defined at x = 0. Also the graph of this function lies in I and III
Quadrants. When x > 0, then y approaches for small values of x and approaches zero as
x approaches .
Similarly, when x < 0, then y approaches – as x approaches zero and approaches zero as
x approaches – . The broad graph of the function is shown in Figure 6.5.
Example
Find inverse of the following functions and show that their graphs are symmetrical about the
line y = x.
1
2
(a) y x 2 (b) y = x , x 0
3
Solution:
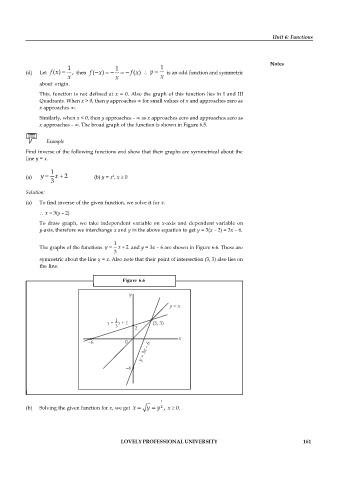
(a) To find inverse of the given function, we solve it for x.
x = 3(y – 2)
To draw graph, we take independent variable on x-axis and dependent variable on
y-axis, therefore we interchange x and y in the above equation to get y = 3(x – 2) = 3x – 6.
1
The graphs of the functions y x 2 and y = 3x – 6 are shown in Figure 6.6. These are
3
symmetric about the line y = x. Also note that their point of intersection (3, 3) also lies on
the line.
Figure 6.6
1
y = x + 2 (3, 3)
3 2
–6 0
– 6
= 3
–6
1
(b) Solving the given function for x, we get x y y 2 , x 0.
LOVELY PROFESSIONAL UNIVERSITY 161