Page 41 - DCAP601_SIMULATION_AND_MODELING

Unit 2: Simulation of Continuous System (I)

b(t) = b(0) + [k .c(0) – k .a(0).b(0)]t Notes
2 1
c(t) = c(0) + [2k .a(0).b(0) – 2k .c(0)]t
1 2
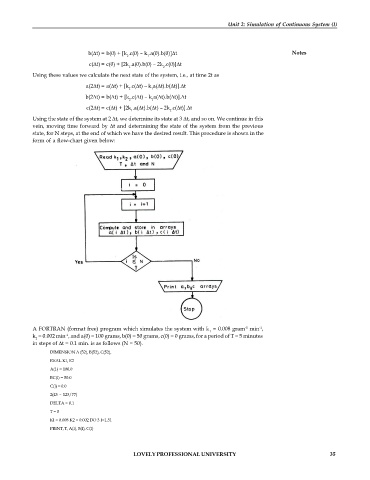
Using these values we calculate the next state of the system, i.e., at time 2t as
a(2t) = a(t) + [k .c(t) – k a(t).b(t)].t
2 1
b(2t) = b(t) + [k .c(t) – k a(t).b(t)].t
2 1
c(2t) = c(t) + [2k .a(t).b(t) – 2k .c(t)].t
1 2
Using the state of the system at 2 t, we determine its state at 3 t, and so on. We continue in this
vein, moving time forward by t and determining the state of the system from the previous
state, for N steps, at the end of which we have the desired result. This procedure is shown in the
form of a flow-chart given below:

-1
A FORTRAN (format free) program which simulates the system with k = 0.008 gram min ,
-1
1
k = 0.002 min , and a(0) = 100 grams, b(0) = 50 grams, c(0) = 0 grams, for a period of T = 5 minutes
-1
2
in steps of t = 0.1 min. is as follows (N = 50).
DIMENSION A (52), B(52), C(52),
REAL KI, K2
A(1) = 100.0
BC(l) = 50.0
C(l) = 0.0
2(45 – 123/77)
DELTA = 0.1
T = 0
Kl = 0.008 K2 = 0.002 DO 3 I=1,51
PRINT, T, A(I), B(I), C(I)

LOVELY PROFESSIONAL UNIVERSITY 35