Page 287 - DCAP605_ADVANCED_DATA_STRUCTURE_AND_ALGORITHMS

Advanced Data Structure and Algorithms

3
Notes Consider that p = k – 1. In this case n = 6k – 2 and a = k . So, one can verify that a ~ n /216. In Zadeh
3
3
3
presents examples of networks that require n /27 and n /12 augmentations, but these examples
are dependent on a choice of the shortest path.
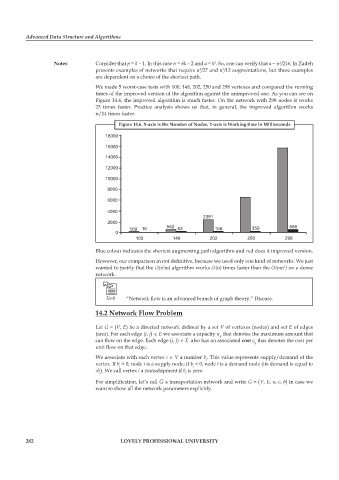
We made 5 worst-case tests with 100, 148, 202, 250 and 298 vertexes and compared the running
times of the improved version of the algorithm against the unimproved one. As you can see on
Figure 14.6, the improved algorithm is much faster. On the network with 298 nodes it works
23 times faster. Practice analysis shows us that, in general, the improved algorithm works
n/14 times faster.

Figure 14.6. X-axis is the Number of Nodes. Y-axis is Working time in Milliseconds
18000

16000
14000
12000

10000
8000
6000

4000
2391
2000
109 15 562 63 156 359 688
0
100 148 202 250 298
Blue colour indicates the shortest augmenting path algorithm and red does it improved version.

However, our comparison in not definitive, because we used only one kind of networks. We just
wanted to justify that the O(n m) algorithm works O(n) times faster than the O(nm ) on a dense
2
2
network.

“Network flow is an advanced branch of graph theory.” Discuss.

14.2 Network Flow Problem

Let G = (V, E) be a directed network defined by a set V of vertexes (nodes) and set E of edges
(arcs). For each edge (i, j) ∈ E we associate a capacity u that denotes the maximum amount that
ij

can flow on the edge. Each edge (i, j) ∈ E also has an associated cost c that denotes the cost per
ij
unit flow on that edge.

We associate with each vertex i ∈ V a number b . This value represents supply/demand of the
i
vertex. If b > 0, node i is a supply node; if b < 0, node i is a demand node (its demand is equal to
i i
-b ). We call vertex i a transshipment if b is zero.
i i
For simplification, let’s call G a transportation network and write G = (V, E, u, c, b) in case we

want to show all the network parameters explicitly.

282 LOVELY PROFESSIONAL UNIVERSITY