Page 68 - DCAP605_ADVANCED_DATA_STRUCTURE_AND_ALGORITHMS

Unit 3: Stacks

3.3.1 Maze Problem Notes

In a classical experimentation in psychology, a rat is placed through the door of a large box in
which walls are set up to restrict movements in most directions. The rat’s movement is observed

as it finds out, through the obstacles, a way to escape from the box. A two-dimensional version
of this problem is easy to formulate where a rectangular maze is conceived as consisting of a
number of unit square rooms such that movement from one square to another is restricted.
An m by n maze can be represented by an array maze of size [1..m, 1..n] where each maze[i,j]
represents a unit room. If maze[i,j] is 0 the room may be entered into but it cannot be entered if
maze[i,j] is 1. The entrance is at maze[1,1] and the exit is at maze[m,n].

Evaluation of Expressions

One of the biggest technical hurdles faced when conceiving the idea of higher level Programming
Languages, is to generate machine language instructions, which would properly evaluate any
arithmetic expression. A complex assignment statement such as:
z -> x / y * * a + b * c – x * a

might have several meanings; even if it were uniquely defined, by the full use of parenthesis.
An expression is made up of operands, operators and delimiters. The above expression has fi ve

operands x, y, a, b and c. The first problem with understanding the meaning of an expression
is to decide in what order the operations are carried out. This means that every language must

uniquely define such an order. To fix the order of evaluation we assign to each operator a priority.
A set of sample priorities are as follows:
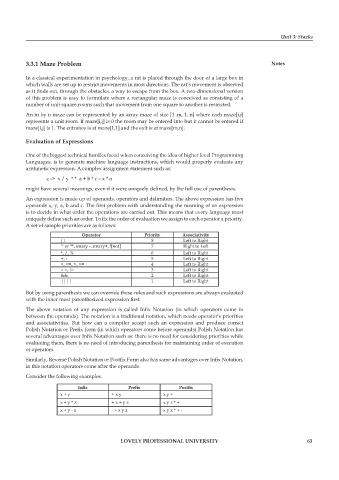
Operator Priority Associativity
( ) 8 Left to Right
^ or **, unary -, unary+, ![not] 7 Right to Left
*, /, % 6 Left to Right
+, - 5 Left to Right
<, <=, >, >= 4 Left to Right
= =, != 3 Left to Right
&& 2 Left to Right
¦¦|| 1 Left to Right

But by using parenthesis we can override these rules and such expressions are always evaluated
with the inner most parenthesized expression fi rst.

The above notation of any expression is called Infix Notation (in which operators come in
between the operands). The notation is a traditional notation, which needs operator’s priorities
and associativities. But how can a compiler accept such an expression and produce correct
Polish Notation or Prefix form (in which operators come before operands) Polish Notation has

several advantages over Infix Notation such as: there is no need for considering priorities while
evaluating them, there is no need of introducing parenthesis for maintaining order of execution
of operators.

Similarly, Reverse Polish Notation or Postfix Form also has same advantages over Infi x Notation,
in this notation operators come after the operands.
Consider the following examples.
Infi x Prefi x Postfi x
x + y + x y x y +
x + y * z + x + y z x y z * +
x + y - z - + x y z x y z * + -

LOVELY PROFESSIONAL UNIVERSITY 63