Page 237 - DMTH201_Basic Mathematics-1
P. 237
Basic Mathematics – I
Notes
If but f(a) is not defined then the discontinuity at x=a can be removed by defining
f(a)=L.
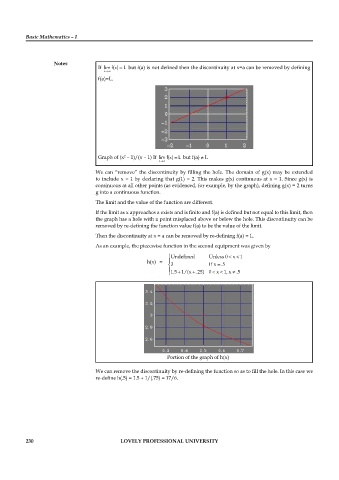
Graph of (x – 1)/(x – 1) If but f(a) L
2
We can “remove” the discontinuity by filling the hole. The domain of g(x) may be extended
to include x = 1 by declaring that g(1) = 2. This makes g(x) continuous at x = 1. Since g(x) is
continuous at all other points (as evidenced, for example, by the graph), defining g(x) = 2 turns
g into a continuous function.
The limit and the value of the function are different.
If the limit as x approaches a exists and is finite and f(a) is defined but not equal to this limit, then
the graph has a hole with a point misplaced above or below the hole. This discontinuity can be
removed by re-defining the function value f(a) to be the value of the limit.
Then the discontinuity at x = a can be removed by re-defining f(a) = L.
As an example, the piecewise function in the second equipment was given by
h(x) =
Portion of the graph of h(x)
We can remove the discontinuity by re-defining the function so as to fill the hole. In this case we
re-define h(.5) = 1.5 1/(.75) = 17/6.
230 LOVELY PROFESSIONAL UNIVERSITY