Page 146 - DCOM203_DMGT204_QUANTITATIVE_TECHNIQUES_I

Unit 7: Measures of Dispersion

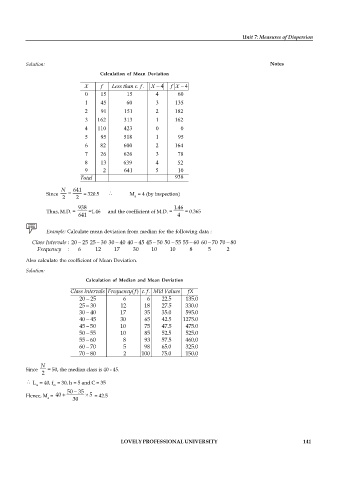
Solution: Notes
Calculation of Mean Deviation
.
X f Less than c f . X 4 f X 4
0 15 15 4 60
1 45 60 3 135
2 91 151 2 182
3 162 313 1 162
4 110 423 0 0
5 95 518 1 95
6 82 600 2 164
7 26 626 3 78
8 13 639 4 52
9 2 641 5 10
Total 938

N 641
Since = 320.5 M = 4 (by inspection)
2 2 d
938 1 46
.
Thus, M.D. = =1.46 and the coefficient of M.D. = = 0.365
641 4
Example: Calculate mean deviation from median for the following data :

Class Intervals : 20 25 25 30 30 40 40 45 45 50 50 55 55 60 60 70 70 80
Frequency : 6 12 17 30 10 10 8 5 2

Also calculate the coefficient of Mean Deviation.
Solution:
Calculation of Median and Mean Deviation
Class Intervals Frequency f) c f Mid Values fX
(
.
.
20 25 6 6 22 .5 135 .0
25 30 12 18 27 .5 330 .0
30 40 17 35 35 .0 595 .0
40 45 30 65 42 .5 1275 .0
45 50 10 75 47 .5 475 .0
50 55 10 85 52 .5 525 .0
55 60 8 93 57 .5 460 .0
60 70 5 98 65 .0 325 .0
70 80 2 100 75 .0 150 .0

N
Since = 50, the median class is 40 - 45.
2
L = 40, f = 30, h = 5 and C = 35
m m
50 35
Hence, M = 40 5 = 42.5
d 30

LOVELY PROFESSIONAL UNIVERSITY 141