Page 190 - DCOM303_DMGT504_OPERATION_RESEARCH

Unit 9: Game Theory

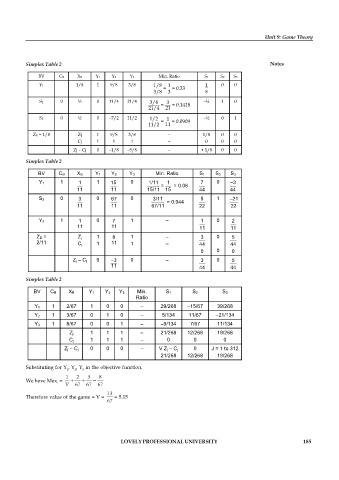
Simplex Table 2 Notes
BV CB XB Y1 Y2 Y3 Min. Ratio S1 S2 S3
Y1 1/8 1 9/8 3/8 1/8 1 1 0 0
3/8 = 3 = 0.33 8
S2 0 ¾ 0 11/4 21/4 3/4 3 –¼ 1 0
21/4 = 21 = 0.1418

S3 0 ½ 0 –7/2 11/2 1/2 1 –½ 0 1
11/2 = 11 = 0.0909
ZB = 1/8 Zj 1 9/8 3/8 – 1/8 0 0
Cj 1 1 1 – 0 0 0
Zj – Cj 0 –1/8 –5/8 – + 1/8 0 0

Simplex Table 2

BV C B X B Y 1 Y 2 Y 3 Min. Ratio S 1 S 2 S 3
Y 1 1 1 1 15 0 1/11 1 7 0 –3
= = 0.06
11 11 15/11 15 44 44
S 2 0 3 0 67 0 3/11 5 1 –21
= 0.044
11 11 67/11 22 22

Y 3 1 1 0 7 1 – 1 0 2
11 11 11 11

Z B = Z j 1 8 1 – 3 0 5
2/11 C j 1 11 1 – 44 44
0 0 0
Z j – C j 0 –3 0 – 3 0 5
11 44 44

Simplex Table 2

BV C B X B Y 1 Y 2 Y 3 Min. S 1 S 2 S 3
Ratio
Y 1 1 2/67 1 0 0 – 29/268 –15/67 39/268
Y 2 1 3/67 0 1 0 – 5/134 11/67 –21/134
Y 3 1 8/67 0 0 1 – –9/134 7/67 11/134
Z j 1 1 1 – 21/268 12/268 19/268
C j 1 1 1 – 0 0 0
Z j – C j 0 0 0 – V Z j – C j 0 J = 1 to 312
21/268 12/268 19/268

Substituting for Y , Y , Y in the objective function.
1 2 3
We have Max. =   

Therefore value of the game = V = = 5.15

LOVELY PROFESSIONAL UNIVERSITY 185