Page 66 - DCOM303_DMGT504_OPERATION_RESEARCH

Unit 3: Linear Programming Problem – Simplex Method

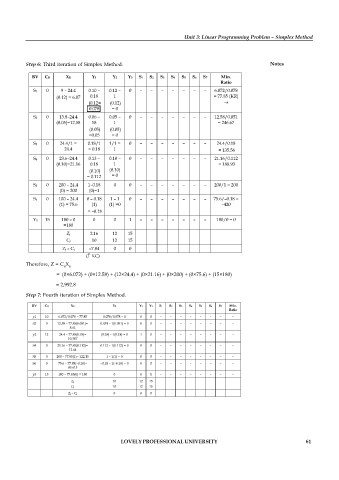
Step 6: Third iteration of Simplex Method. Notes
BV CB XB Y1 Y2 Y3 S1 S2 S3 S4 S5 S6 S7 Min.
Ratio
S1 0 9 – 24.4 0.10 – 0.12 – 0 – – – – – – – 6.072/0.078
(0.12) = 6.07 0.18 1 = 77.85 (KR)
(0.12= (0.12) 
0.078 = 0
S2 0 13.8–24.4 0.06 – 0.05 – 0 – – – – – – – 12.58/0.051
(0.05)=12.58 18 1 = 246.67
(0.05) (0.05)
=0.05 = 0
S3 0 24.4/1 = 0.18/1 1/1 = 0 – – – – – – – 24.4/0.18
24.4 = 0.18 1 = 135.56
S4 0 23.6–24.4 0.13 – 0.10 – 0 – – – – – – – 21.16/0.112
(0.10)=21.16 0.18 1 = 188.93
(0.10) (0.10)
= 0.112 = 0
S5 0 200 – 24.4 1–0.18 0 0 – – – – – – – 200/1 = 200
(0) = 200 (0)=1
S6 0 100 – 24.4 0 – 0.18 1 – 1 0 – – – – – – – 75.6/–0.18 =
(1) = 75.6 (1) (1) =0 –420
= –0.18
Y3 15 180 – 0 0 0 1 – – – – – – – 180/0 = 0
=180
Zj 2.16 12 15
Cj 10 12 15
Zj – Cj –7.84 0 0
( KC)
Therefore, Z = C X
B B
= (0×6.072) + (0×12.58) + (12×24.4) + (0×21.16) + (0×200) + (0×75.6) + (15×180)
= 2,992.8
Step 7: Fourth iteration of Simplex Method.

BV CB XB Y1 Y2 Y3 S1 S2 S3 S4 S5 S6 S7 Min.
Ratio
y1 10 6.072/0.078 = 77.85 0.078/0.078 = 1 0 0 – – – – – – – –
S2 0 12.58 – 77.85(0.051)= 0.051 – 1(0.051) = 0 0 0 – – – – – – – –
8.61
y2 12 24.4 – 77.85(0.18)= (0.18) – 1(0.18) = 0 1 0 – – – – – – – –
10.387
S4 0 21.16 – 77.85(0.112)= 0.112 – 1(0.112) = 0 0 0 – – – – – – – –
12.44
S5 0 200 – 77.85(1)= 122.15 1 – 1(1) = 0 0 0 – – – – – – – –
S6 0 75.6 – 77.85(–0.18)= –0.18 – 1(–0.18) = 0 0 0 – – – – – – – –
89.613
y3 15 180 – 77.85(0) = 180 0 0 1 – – – – – – – –
Zj 10 12 15
Cj 10 12 15
Zj – Cj 0 0 0

LOVELY PROFESSIONAL UNIVERSITY 61