Page 26 - DMGT515_PERSONAL_FINANCIAL_PLANNING

Unit 2: Time Value of Money

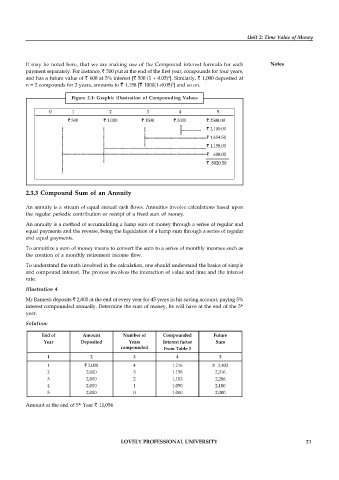
It may be noted here, that we are making use of the Compound interest formula for each Notes
payment separately. For instance, ` 500 put at the end of the first year, compounds for four years,
4
and has a future value of ` 608 at 5% interest [` 500 (1 + 0.05) ]. Similarly, ` 1,000 deposited at
3
n = 2 compounds for 3 years, amounts to ` 1,158 [` 1000(1+0.05) ] and so on.
Figure 2.1: Graphic illustration of Compounding Values

0 1 2 3 4 5
` 500 ` 1,000 ` 1500 ` 2000 ` 2500.00
` 2,100.00
` 1,654.50
` 1,158.00
` 608.00
` 8020.50

2.3.3 Compound Sum of an Annuity

An annuity is a stream of equal annual cash flows. Annuities involve calculations based upon
the regular periodic contribution or receipt of a fixed sum of money.

An annuity is a method of accumulating a lump sum of money through a series of regular and
equal payments and the reverse, being the liquidation of a lump sum through a series of regular
and equal payments.
To annuitize a sum of money means to convert the sum to a series of monthly incomes such as
the creation of a monthly retirement income flow.
To understand the math involved in the calculation, one should understand the basics of simple
and compound interest. The process involves the interaction of value and time and the interest
rate.
Illustration 4
Mr Ramesh deposits ` 2,000 at the end of every year for 45 years in his saving account, paying 5%
interest compounded annually. Determine the sum of money, he will have at the end of the 5 th
year.
Solution:

End of Amount Number of Compounded Future
Year Deposited Years Interest factor Sum
compounded From Table 3
1 2 3 4 5
1 ` 2,000 4 1.216 8 2,432
2 2,000 3 1.158 2,316
3 2,000 2 1.103 2,206
4 2,000 1 1.050 2,100
5 2,000 0 1.000 2,000
th
Amount at the end of 5 Year ` 11,054

LOVELY PROFESSIONAL UNIVERSITY 21