Page 71 - DCOM203_DMGT204_QUANTITATIVE_TECHNIQUES_I

Quantitative Techniques – I

Notes
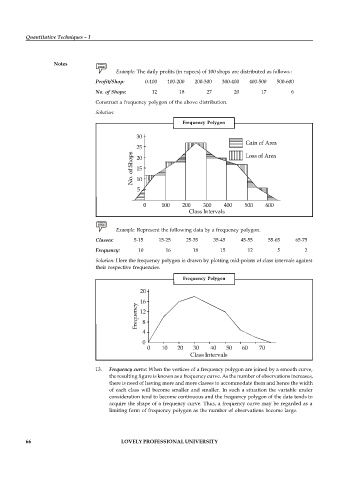
Example: The daily profits (in rupees) of 100 shops are distributed as follows :
Profit/Shop: 0-100 100-200 200-300 300-400 400-500 500-600

No. of Shops: 12 18 27 20 17 6
Construct a frequency polygon of the above distribution.
Solution:
Frequency Polygon

Example: Represent the following data by a frequency polygon.
Classes: 5-15 15-25 25-35 35-45 45-55 55-65 65-75
Frequency: 10 16 18 15 12 5 2

Solution: Here the frequency polygon is drawn by plotting mid-points of class intervals against
their respective frequencies.

Frequency Polygon

13. Frequency curve: When the vertices of a frequency polygon are joined by a smooth curve,
the resulting figure is known as a frequency curve. As the number of observations increases,
there is need of having more and more classes to accommodate them and hence the width
of each class will become smaller and smaller. In such a situation the variable under
consideration tend to become continuous and the frequency polygon of the data tends to
acquire the shape of a frequency curve. Thus, a frequency curve may be regarded as a
limiting form of frequency polygon as the number of observations become large.

66 LOVELY PROFESSIONAL UNIVERSITY