Page 32 - DECO403_MATHEMATICS_FOR_ECONOMISTS_PUNJABI

noEPk;soh dk rfDs

B'N d'^bx[rDe cbB dk ;XkoD ;wheoD j/m nB[;ko j[zdk j?^

x
(id'A fe A = e )
fJ; cbB dhnK w[Zy ftP/PsktK fBwB fbys jB^

A
(i) i/eo β & 1 T[d'A y = iK xy = A
x
(T[d'A fJj nkfJs gotb j' ikJ/rk)
(ii) i/eo β < 1 j? sK x d/ tXD d/ Bkb y tZXdh do Bkb tZXdk j?.
(iii) i/eo 0 < β < 1 j? sK x d/ tXD d/ Bkb y xNdh do s'A tZXdk j?.

(iv) i/eo β < 0 j? sK x tXD d/ Bkb y xNdk j?.
fJZE/ fJj T[b/y:'r j? fe xBkswe xks T[sgkdB cbB ns/ foDkswe xks wzr ftPb/PD ftZu
T[fus j[zdhnK jB. fJjBK dh gqw[Zy ftP/Psk fJj j? fe xksKe ;fEo b'u B{z do;kT[Ad/ jB.
(;) xksh cbB (Exponential Function) L xksh cbB th noEPk;so ftZu pj[s T[g:'rh j?.
fJ; cbB ftZu y, x dk cbB Bk j' e/ x d/ xksh dk cbB j[zdk j?. fJ;B{z fBwB fbys
;wheoDK d[nkok do;kfJnk ik ;edk j?^
x
y = log e x, y = e , y = e sinx
nkfd
x
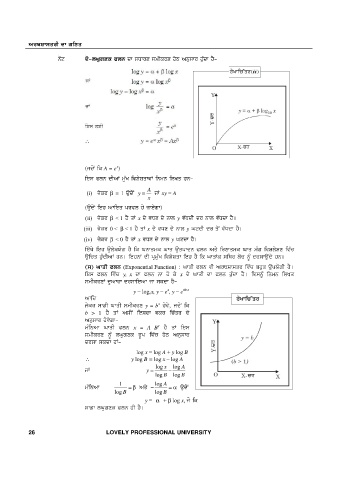
i/eo ;kvh xksh ;wheoD y = b j't/, id'A fe
b > 1 j? sK n;hA fJ;dk teo fuZso d/
nB[;ko j't/rk^
y
wzfBnk xksh cbB x = A B j? sK fJ;
;wheoD B{z bx[rDe o{g ftZu j/m nB[;ko
do;k ;edk jK^
log x = log A + y log B
∴ y log B = log x – log A
log x log A
iK y = −
log B log B
1 log A
wzfBnk =β ns/ − =α T[d'A
log B log B
y = α + β log x, i' fe
;kvk bx[rDe cbB jh j?.

26 LOVELY PROFESSIONAL UNIVERSITY