Page 195 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_ENGLISH

Unit 13: Coefficient of Simple Regression Method

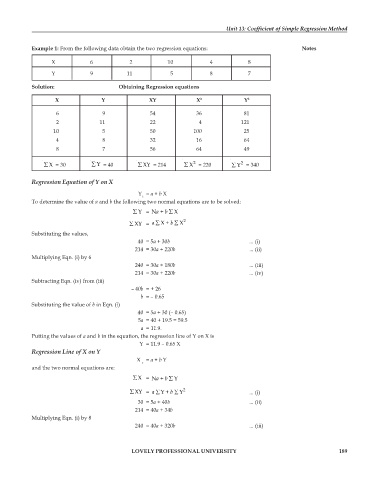
Example 1: From the following data obtain the two regression equations: Notes

X 6 2 10 4 8
Y 9 11 5 8 7

Solution: Obtaining Regression equations

X Y XY X 2 Y 2

6 9 54 36 81
2 11 22 4 121
10 5 50 100 25
4 8 32 16 64
8 7 56 64 49

2
2
∑ X = 30 ∑ Y = 40 ∑ XY = 214 ∑ X = 220 ∑ Y = 340
Regression Equation of Y on X
Y = a + b X
c
To determine the value of a and b the following two normal equations are to be solved:
a
∑ Y = N + b ∑ X
∑ XY = ∑ a ∑ X + b X 2

Substituting the values,
40 = 5a + 30b ... (i)
214 = 30a + 220b ... (ii)
Multiplying Eqn. (i) by 6
240 = 30a + 180b ... (iii)
214 = 30a + 220b ... (iv)
Subtracting Eqn. (iv) from (iii)
– 40b = + 26
b = – 0.65
Substituting the value of b in Eqn. (i)
40 = 5a + 30 (– 0.65)
5a = 40 + 19.5 = 59.5
a = 11.9.
Putting the values of a and b in the equation, the regression line of Y on X is
Y = 11.9 – 0.65 X
Regression Line of X on Y
X = a + b Y
c
and the two normal equations are:
∑ X = N + a b ∑ Y

∑ XY = ∑ a ∑ Y + b Y 2 ... (i)
30 = 5a + 40b ... (ii)
214 = 40a + 34b
Multiplying Eqn. (i) by 8
240 = 40a + 320b ... (iii)

LOVELY PROFESSIONAL UNIVERSITY 189