Page 113 - DMTH401_REAL ANALYSIS

Unit 9: Functions

Through the point A = (1, 0); we draw a vertical line labeled as t-axis with origin at A and Notes
positive direction upwards. Now, let t be any real number and we will think of this as a point on
this verticle number line i.e., t-axis.
Imagine this t-axis as a line of thread that can be wrapped around the circle C. Let p(t) = (x, y) be
the point where ‘t’ ends up when this wrapping takes place. In other words, the line segment
from A to point (t, 0) becomes the arc from A to P, positive or negative i.e., counterclockwise or
clockwise, depending on whether t > 0 or t < 0. Of course, when t = 0, P = A. Then, the trigonometric
functions 'sine' and 'cosine', for arbitrary t R, are defined by
sin t = sin  = y, and cos t = cos  = x,

where '' is the radian measure of the angle subtended by the arc AP at the centre of the circle C.
More generally, if t is any real number, we may take (0 <  < 2) to be the angle (rotation) whose
radian measure is t. It is then clear that
sin (t + 2) = sin t and cos (t + 2) = cos t.

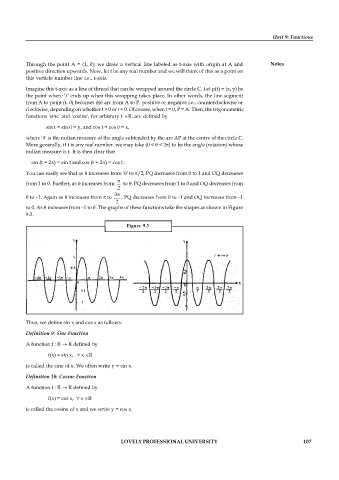
You can easily see that as  increases from '' to /2, PQ increases from 0 to 1 and OQ decreases

from 1 to 0. Further, as increases from to , PQ decreases from 1 to 0 and OQ decreases from
2
3
0 to –1. Again as  increases from  to , PQ decreases from 0 to –1 and OQ increases from –1
2
to 0. As  increases from –1 to 0. The graphs of these functions take the shapes as shown in Figure
9.3.

Figure 9.3

Thus, we define sin x and cos x as follows:

Definition 9: Sine Function
A function f : R  R defined by
f(x) = sin x, " x R

is called the sine of x. We often write y = sin x.
Definition 10: Cosine Function
A function f : R  R defined by

f(x) = cos x, " x R
is called the cosine of x and we write y = cos x.

LOVELY PROFESSIONAL UNIVERSITY 107