Page 117 - DMTH401_REAL ANALYSIS

Unit 9: Functions

Notes
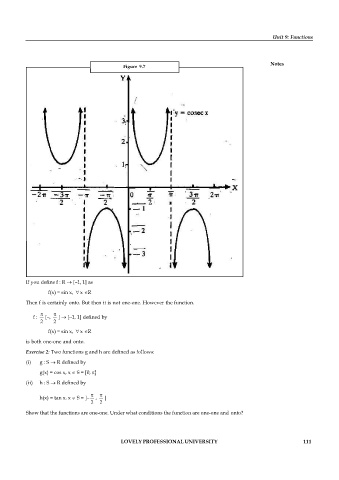
Figure 9.7

If you define f : R  [–1, 1] as

f(x) = sin x, " x R
Then f is certainly onto. But then it is not one-one. However the function.
 
f : [–, ] [–1, 1] defined by
2 2
f(x) = sin x, " x R
is both one-one and onto.

Exercise 2: Two functions g and h are defined as follows:
(i) g : S  R defined by
g(x) = cos x, x S = [0, ]
(ii) h : S  R defined by

 
h(x) = tan x, x S = ]– , [
2 2
Show that the functions are one-one. Under what conditions the function are one-one and onto?

LOVELY PROFESSIONAL UNIVERSITY 111