Page 121 - DMTH401_REAL ANALYSIS

Unit 9: Functions

Notes
Example: Let f : S  T be a strictly increasing function such that f(S) = T. Then prove that
f is invertible and f : T  S is also strictly increasing.
1
Solution:

Since f : S  T is strictly increasing, therefore, f is one-one. Further, since f (S) = T, therefore f is
–1
onto. Thus f is one-one and onto. Hence f is invertible. In other words, f : T  S exists.
Now, for any y , y T, we have y = f(x ), y – f(x ). If y < y ) then we claim x < x .
1 2 1 1 2 2 1 2 1 2
Indeed if x  x , then f(x )  f(x ) (why?).
1 2 1 2
This implies that y  y which contradicts that y < y .
1 2 1 2
–1
Hence y < y  x < x f (y ) < f (y )
–1
1 2 1 2 1 2
–1
which shows that f is strictly increasing.
You can similarly solve the following exercise for a strictly decreasing function:
Exercise 3: Let f : S  T be a strictly decreasing function such that f(S) = T. Show that f is invertible
and f : T S is also strictly decreasing.
–1
9.3.2 Logarithmic Function

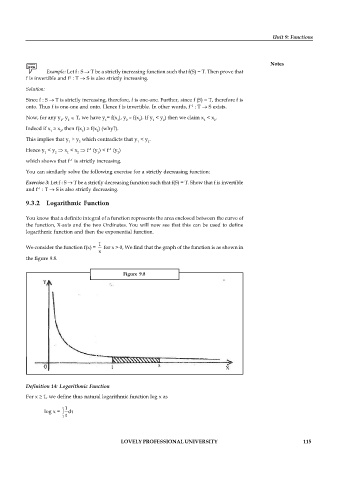
You know that a definite integral of a function represents the area enclosed between the curve of
the function, X-axis and the two Ordinates. You will now see that this can be used to define
logarithmic function and then the exponential function.

1
We consider the function f(x) = for x > 0, We find that the graph of the function is as shown in
x
the figure 9.8.

Figure 9.8

Definition 14: Logarithmic Function
For x  1, we define thus natural logarithmic function log x as

x 1
log x = ò dt
1 t

LOVELY PROFESSIONAL UNIVERSITY 115