Page 122 - DMTH401_REAL ANALYSIS

Real Analysis

Notes 1
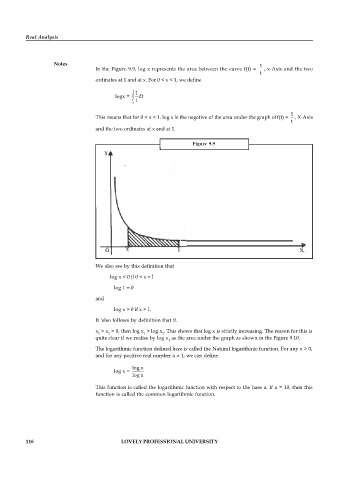
In the Figure 9.9, log x represents the area between the curve f(t) = , x-Axis and the two
t
ordinates at 1 and at x. For 0 < x < 1, we define

1 1
logx = ò dt
x t
1
This means that for 0 < x < 1. log x is the negative of the area under the graph of f(t) = , X-Axis
t
and the two ordinates at x and at 1.

Figure 9.9

We also see by this definition that
log x < 0 if 0 < x < l

log 1 = 0
and
log x > 0 if x > 1.

It 'also follows by definition that if.
x > x > 0, then log x > log x . This shows that log x is strictly increasing. The reason for this is
1 2 1 2
quite clear if we realise by log x as the area under the graph as shown in the Figure 9.10.
1
The logarithmic function defined here is called the Natural logarithmic function. For any x > 0,
and for any positive real number a  1, we can define
log x
log x =
log a
This function is called the logarithmic function with respect to the base a. If a = 10, then this
function is called the common logarithmic function.

116 LOVELY PROFESSIONAL UNIVERSITY