Page 124 - DMTH401_REAL ANALYSIS

Real Analysis

Notes 9.3.3 Exponential Function

We now come to define exponential function. We have seen that
log x : ]0, [ R
is strictly increasing function. The graph of the logarithmic function also shows that

log x : ]0, [ R
is also onto. Therefore this function admits of inverse function. Its inverse function, called the
Exponential function, Exp (x) has domain as the set R of all real numbers and range as ]0, [. If

log x = y, then Exp (y) = x.
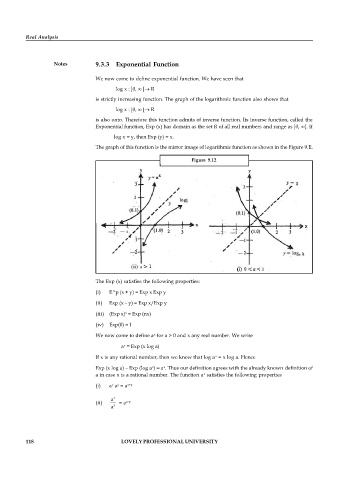
The graph of this function is the mirror image of logarithmic function as shown in the Figure 9.12.

Figure 9.12

The Exp (x) satisfies the following properties:

(i) E^p (x + y) = Exp x Exp y
(ii) Exp (x – y) = Exp x/Exp y
n
(iii) (Exp x) = Exp (nx)
(iv) Exp(0) = 1
x
We now come to define a for a > 0 and x any real number. We write
a = Exp (x log a)
x
x
If x is any rational number, then we know that log a = x log a. Hence
x
x
Exp (x log a) – Exp (log a ) = a . Thus our definition agrees with the already known definition of
x
a in case x is a rational number. The function a satisfies the following properties
(i) a a = a x+y
x
y
a x
(ii) = a x–y
a y

118 LOVELY PROFESSIONAL UNIVERSITY