Page 178 - DMTH401_REAL ANALYSIS

Real Analysis

Notes

Task Consider the following functions:

2
ì x - 9
ï if x ¹ 3
1. k(x) = í x 3
-
ï 1, if x = 3
î
>
ì 1, if x 0
ï
2. h(x) = í 0, If x = 0
ï
<
î - 1, if x 0
ì sin(1/x), if x ¹ 0
3. f(x) = í
î 0, If x ¹ 0

ì 1, if x = rational
4. g(x) = í
î 0, If x = irrational
Which of these functions, without proof, has a ‘fake’ discontinuity, a ‘regular’ discontinuity,
or a ‘difficult’ discontinuity?

13.2 Classification of Discontinuities

Suppose f is a function with domain D and c  D is a point of discontinuity of f.
1. If limf(x) exists, then c is called removable discontinuity.
x® c

2. If limf(x) does not exist, but both lim f(x) and lim f(x) exist, then c is called a discontinuity
x® c x® c - x® c +
of the first kind, or jump discontinuity.
3. If either lim f(x) or lim f(x) does not exist, then c is called a discontinuity of the second
x® c - x® c +
kind, or essential discontinuity.

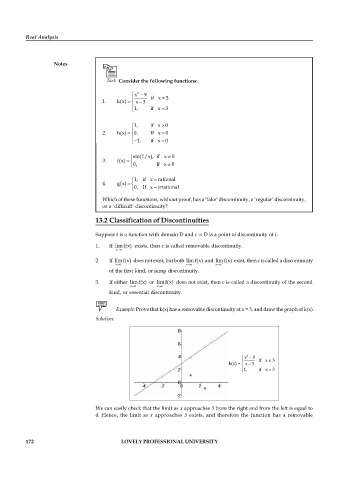
Example: Prove that k(x) has a removable discontinuity at x = 3, and draw the graph of k(x).
Solution:

x 2 9
if x 3
k(x) x 3
1, if x 3

We can easily check that the limit as x approaches 3 from the right and from the left is equal to
4. Hence, the limit as x approaches 3 exists, and therefore the function has a removable

172 LOVELY PROFESSIONAL UNIVERSITY