Page 182 - DMTH401_REAL ANALYSIS

Real Analysis

Notes In other words, f must look pretty bad if it has a discontinuity of the second kind.

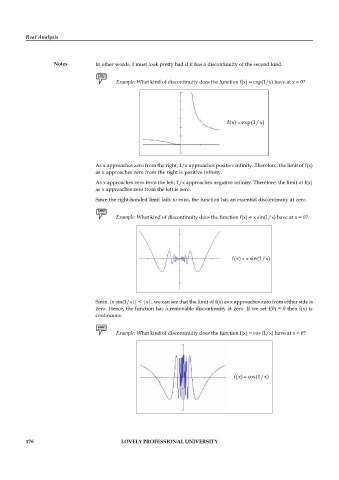
Example: What kind of discontinuity does the function f(x) = exp(1/x) have at x = 0?

f(x) exp(1/x)

As x approaches zero from the right, 1/x approaches positive infinity. Therefore, the limit of f(x)
as x approaches zero from the right is positive infinity.

As x approaches zero from the left, 1/x approaches negative infinity. Therefore, the limit of f(x)
as x approaches zero from the left is zero.
Since the right-handed limit fails to exist, the function has an essential discontinuity at zero.

Example: What kind of discontinuity does the function f(x) = x sin(1/x) have at x = 0?

f(x) x sin(1/x)

Since |x sin(1/x)| < |x|, we can see that the limit of f(x) as x approaches zero from either side is
zero. Hence, the function has a removable discontinuity at zero. If we set f(0) = 0 then f(x) is
continuous.

Example: What kind of discontinuity does the function f(x) = cos (1/x) have at x = 0?

f(x) cos(1/x)

176 LOVELY PROFESSIONAL UNIVERSITY