Page 187 - DMTH401_REAL ANALYSIS

Unit 14: Sequences and Series of Functions

Notes
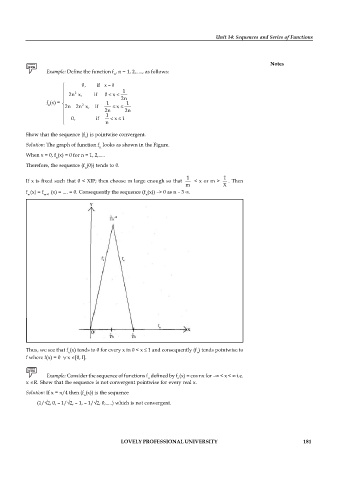
Example: Define the function f , n = 1, 2,....., as follows:
n
ì 0, if x = 0
ï 1
2
ï 2n x, if 0 < x <
ï 2n
f (x) = í 1 1
2
n 2n - 2n x, if  x 
ï 2n 2n
ï 1
ï 0, if < x  1
î n
Show that the sequence (f ) is pointwise convergent.
n
Solution: The graph of function f looks as shown in the Figure.
n
When x = 0, f (x) = 0 for n = 1, 2,.....
n
Therefore, the sequence (f (0)) tends to 0.
n
1 1
If x is fixed such that 0 < XIP; then choose m large enough so that < x or m > . Then
m X
f (x) = f (x) = .... = 0. Consequently the sequence (f (x)) –> 0 as n – 3 ¥.
m m+1 n

Thus, we see that f (x) tends to 0 for every x in 0 < x  1 and consequently (f ) tends pointwise to
n n
f where f(x) = 0 " x [0, I].

Example: Consider the sequence of functions f defined by f (x) = cos nx for –¥ < x < ¥ i.e.
n n
x R. Show that the sequence is not convergent pointwise for every real x.
Solution: If x = /4 then (f (x)) is the sequence
n
(1/2, 0, – 1/2, – 1, – 1/2, 0,.....) which is not convergent.

LOVELY PROFESSIONAL UNIVERSITY 181