Page 179 - DMTH401_REAL ANALYSIS

Unit 13: Discontinuities and Monotonic Functions

discontinuity at x = 3. If we define k(3) = 4 instead of k(3) = 1 then the function in fact will be Notes
continuous on the real line

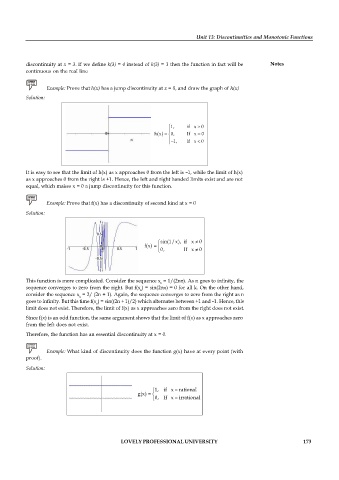
Example: Prove that h(x) has a jump discontinuity at x = 0, and draw the graph of h(x)
Solution:

1, if x 0
h(x) 0, If x 0
1, if x 0

It is easy to see that the limit of h(x) as x approaches 0 from the left is –1, while the limit of h(x)
as x approaches 0 from the right is +1. Hence, the left and right handed limits exist and are not
equal, which makes x = 0 a jump discontinuity for this function.

Example: Prove that f(x) has a discontinuity of second kind at x = 0
Solution:

sin(1/x), if x 0
f(x)
0, If x 0

This function is more complicated. Consider the sequence x = 1/(2n). As n goes to infinity, the
n
sequence converges to zero from the right. But f(x ) = sin(2n) = 0 for all k. On the other hand,
n
consider the sequence x = 2/ (2n + 1). Again, the sequence converges to zero from the right as n
n
goes to infinity. But this time f(x ) = sin((2n + 1)/2) which alternates between +1 and –1. Hence, this
n
limit does not exist. Therefore, the limit of f(x) as x approaches zero from the right does not exist.
Since f(x) is an odd function, the same argument shows that the limit of f(x) as x approaches zero
from the left does not exist.
Therefore, the function has an essential discontinuity at x = 0.

Example: What kind of discontinuity does the function g(x) have at every point (with
proof).
Solution:

1, if x rational
g(x)
0, If x irrational

LOVELY PROFESSIONAL UNIVERSITY 173