Page 234 - DMTH504_DIFFERENTIAL_AND_INTEGRAL_EQUATION

Unit 15: Cauchy’s Problem and Characteristics for First Order Equations

defines a strip at the point (x, y, z) of the curve C. If such a strip is also an integral element of Notes
equation (3), we say that it is an integral strip of equation (3) i.e., the set of functions (7) is an
integral strip of equation (3) provided they satisfy condition (8) and the condition
F(x(t), y(t), z(t), p(t), q(t)) = 0 ...(9)
for all t in l.

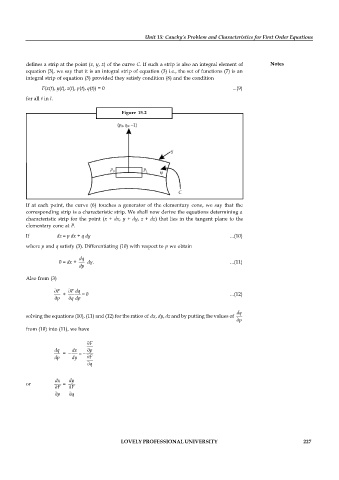
Figure 15.2

If at each point, the curve (6) touches a generator of the elementary cone, we say that the
corresponding strip is a characteristic strip. We shall now derive the equations determining a
characteristic strip for the point (x + dx, y + dy, z + dz) that lies in the tangent plane to the
elementary cone at P.
If dz = p dx + q dy ...(10)

where p and q satisfy (3). Differentiating (10) with respect to p we obtain
dq
0 = dx + dy. ...(11)
dp
Also from (3)

F F dq
+ 0 ...(12)
p q dp

dq
solving the equations (10), (11) and (12) for the ratios of dx, dy, dz and by putting the values of
p
from (10) into (11), we have

F
dq dx p
=
dp dy F
q

dx dy
or =
F F
p q

LOVELY PROFESSIONAL UNIVERSITY 227