Page 154 - DCOM203_DMGT204_QUANTITATIVE_TECHNIQUES_I

Unit 7: Measures of Dispersion

Solution: Notes
It is given that X 60 , = 20 and n = 200
,
The sum of observations 200 60 12 000
To find the sum of squares of observations, we use the relation

X i 2 n 2 X 2

From this we can write X 2 200 400 3600 8,00,000
i
Further the corrected sum of observations ( X ) = uncorrected sum of observations – sum of
i
wrongly recorded observations + sum of correct observations = 12,000 – (3 + 67) + (13 +17)
= 11,960.
11960
Corrected X 59 8
.
200
2
Similarly, the corrected sum of squares ( X ) = uncorrected sum of squares - sum of squares of
i
wrongly recorded observations + sum of squares of correct observations
2
2
2
2
= 8,00,000 – (3 + 67 ) + (13 +17 ) = 7,95,960
795960 2
Hence, corrected 2 = 59.8 403.76 or corrected = 20.09
200
20 09
.
.
Also, CV = 100 33 60.
59 8
.
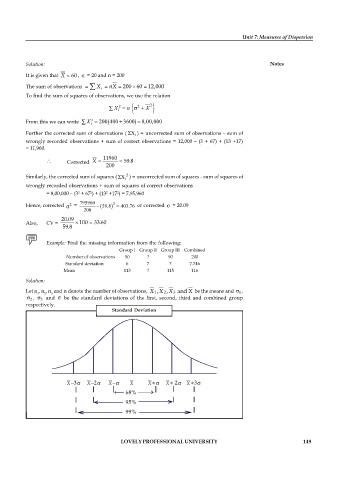
Example: Find the missing information from the following:
Group I Group II Group III Combined
Number of observations 50 ? 90 200
Standard deviation 6 7 ? 7.746
Mean 113 ? 115 116
Solution:
2,
1,
Let n , n , n and n denote the number of observations, X X X 3 and X be the means and 1 ,
1 2 3
2 , 3 and be the standard deviations of the first, second, third and combined group
respectively.
Standard Deviation

–3 –2 – + + 2 +3

68%
95%
99%

LOVELY PROFESSIONAL UNIVERSITY 149