Page 228 - DMGT209_QUANTITATIVE_TECHNIQUES_II

Unit 11: Multiple Regression and Correlation Analysis

Notes
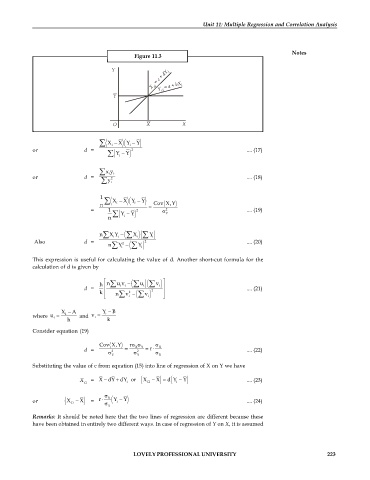
Figure 11.3

Y dY i
c +
=
= +
X ci Y a bX i
ci
Y

O X X

  X  X  Y  Y 
i
i
or d = 2 .... (17)
  Y  Y 
i
 x y i
i
or d = 2 .... (18)
 y i
1
  X  X  Y  Y 
i
i
n  Cov X,Y 
= 1  Y  2  2 Y .... (19)
i
n  Y 
n  X Y   X i  Y i 
i
i
Also d = 2 2 .... (20)
n  Y   Y i 
i
This expression is useful for calculating the value of d. Another short-cut formula for the
calculation of d is given by


h  u v   u i  v i  
n
i
i
d =  2  .... (21)
k  n  v   v  
2
 i i 
X  A Y  B
i
where u  i and v 
i
i
h k
Consider equation (19)
Cov X,Y  r  Y  X
X
d = 2  2  r  .... (22)
 Y  Y  Y
Substituting the value of c from equation (15) into line of regression of X on Y we have
X = X dY dY or   X  X   Y d  Y  .... (23)
Ci i Ci i
 X
or  X  X  = r   Y  Y  Y  .... (24)
i
Ci
Remarks: It should be noted here that the two lines of regression are different because these
have been obtained in entirely two different ways. In case of regression of Y on X, it is assumed

LOVELY PROFESSIONAL UNIVERSITY 223