Page 148 - DCOM303_DMGT504_OPERATION_RESEARCH

Unit 7: Assignment Problem – Balanced

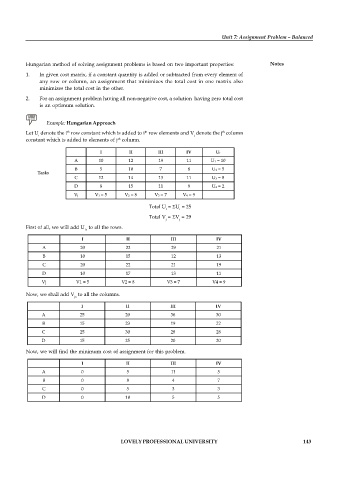
Hungarian method of solving assignment problems is based on two important properties: Notes
1. In given cost matrix, if a constant quantity is added or subtracted from every element of
any row or column, an assignment that minimizes the total cost in one matrix also
minimizes the total cost in the other.
2. For an assignment problem having all non-negative cost, a solution having zero total cost
is an optimum solution.

Example: Hungarian Approach

th
Let U denote the i row constant which is added to i row elements and V denote the j column
th
th
i j
constant which is added to elements of j column.
th
I II III IV Ui
A 10 12 19 11 U1 = 10

B 5 10 7 8 U2 = 5
Tasks
C 12 14 13 11 U3 = 8
D 8 15 11 9 U4 = 2
Vj V1 = 5 V2 = 8 V3 = 7 V4 = 9

Total U = U = 25
i
i
Total V = V = 29
j j
First of all, we will add U to all the rows.
is
I II III IV

A 20 22 29 21
B 10 15 12 13
C 20 22 21 19

D 10 17 13 11

Vj V1 = 5 V2 = 8 V3 = 7 V4 = 9

Now, we shall add V to all the columns.
js
I II III IV
A 25 20 36 30
B 15 23 19 22
C 25 30 28 28
D 15 25 20 20
Now, we will find the minimum cost of assignment for this problem.

I II III IV
A 0 5 11 5
B 0 8 4 7
C 0 5 3 3
D 0 10 5 5

LOVELY PROFESSIONAL UNIVERSITY 143