Page 39 - DCOM303_DMGT504_OPERATION_RESEARCH

Operations Research

Notes Self Assessment

Fill in the blanks:
4. Graphical method can be used only if there are ………………..decision variables.
5. While solving a LP graphically the area bounded by the constraints is called …………….

6. If the given problem is maximization, Z then locate the solution point at the
max
……………point of the feasible zone from the origin
2.7 Minimization Cases of LP

Example: A rubber company is engaged in producing 3 different kinds of tyres A, B and C.
These three different tyres are produced at the company’s 2 different plants with different
production capacities. In a normal 8 hrs working day plant 1 produces 50, 100 and 100 tyres of A,
B and C respectively. Plant 2 produce 60, 60 and 200 tyres of type A, B and C respectively. The
monthly demand for tyre A, B and C is 2,500, 3,000 and 7,000 units respectively. The daily cost of
operation of plant 1 and 2 is ` 2,500 and ` 3,500 respectively. Find the minimum number of days
of operation per month at 2 different plants to minimize the total costs while meeting the
demand.

Solution:
Let x be the daily cost of operation in plant 1
1
x be the daily cost of operation in plant 2
2
Minimize ‘Z’ = 2,500x + 3,500x (Subject to constraints)
1 2
50x + 60x  2,500
1 2
100x + 60x  3,000
1 2
100x + 200x  7,000 (Demand Constraints)
1 2
x , x  0 (Non-negativity constraints)
1 2
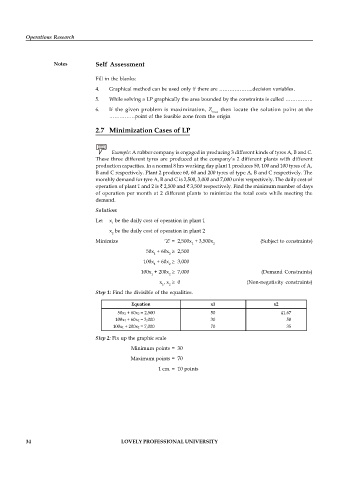
Step 1: Find the divisible of the equalities.
Equation x1 x2
50x1 + 60x2 = 2,500 50 41.67
100x1 + 60x2 = 3,000 30 50
100x1 + 200x2 = 7,000 70 35

Step 2: Fix up the graphic scale
Minimum points = 30
Maximum points = 70
1 cm. = 10 points

34 LOVELY PROFESSIONAL UNIVERSITY