Page 80 - DECO405_MANAGERIAL_ECONOMICS

Unit 5: Elasticity of Demand

Notes
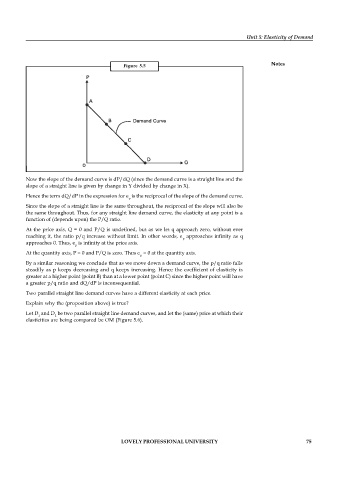
Figure 5.5

Now the slope of the demand curve is dP/dQ (since the demand curve is a straight line and the
slope of a straight line is given by change in Y divided by change in X).
Hence the term dQ/dP in the expression for e is the reciprocal of the slope of the demand curve.
p
Since the slope of a straight line is the same throughout, the reciprocal of the slope will also be
the same throughout. Thus, for any straight line demand curve, the elasticity at any point is a
function of (depends upon) the P/Q ratio.
At the price axis, Q = 0 and P/Q is undefined, but as we let q approach zero, without ever
reaching it, the ratio p/q increase without limit. In other words, e approaches infinity as q
p
approaches 0. Thus, e is infinity at the price axis.
p
At the quantity axis, P = 0 and P/Q is zero. Thus e = 0 at the quantity axis.
p
By a similar reasoning we conclude that as we move down a demand curve, the p/q ratio falls
steadily as p keeps decreasing and q keeps increasing. Hence the coefficient of elasticity is
greater at a higher point (point B) than at a lower point (point C) since the higher point will have
a greater p/q ratio and dQ/dP is inconsequential.
Two parallel straight line demand curves have a different elasticity at each price.
Explain why the (proposition above) is true?
Let D and D be two parallel straight line demand curves, and let the (same) price at which their
1 2
elasticities are being compared be OM (Figure 5.6).

LOVELY PROFESSIONAL UNIVERSITY 75