Page 204 - DMGT405_FINANCIAL%20MANAGEMENT

Financial Management

Notes Limitation: The method does not provide the decision-maker with a concrete value
indicative of variability and therefore risk. The standard deviation and the coefficient
variation are two such measures, which tell us about the variability associated with the
expected cash flow in terms of degree of risk. Standard deviation can be applied when the
project involves the same outlay. If the prospects to be compared involve different outlay,
the coefficient of variation is the correct choice, being a relative measure.
3. Standard Deviation and Co-efficient of variation: In statistical terms, standard deviation
is defined as the square root of the mean of the standard deviations, where deviation is the
difference between an outcome and the expected mean value of all outcomes. Further,
calculate the value of standard deviation after providing weights to the square of each
deviation (its probability of occurrence).
The greater the standard deviation of a probability distribution, the greater is the dispersion
of outcomes around the expected values.
If the two prospects have the same expected value (mean) then one that has the greater
standard deviation will said to have the higher degree of uncertainty or risk.
However, if the size of the project’s outlay differs, the decision-maker should make use of
the coefficient of variation to judge the riskiness of the project.

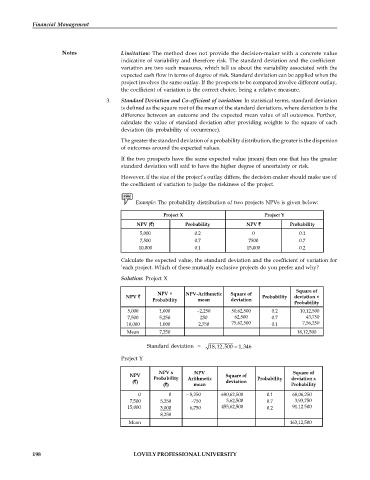
Example: The probability distribution of two projects NPVs is given below:

Project X Project Y
NPV ( ) Probability NPV Probability
5,000 0.2 0 0.1
7,500 0.7 7500 0.7
10,000 0.1 15,000 0.2

Calculate the expected value, the standard deviation and the coefficient of variation for
‘each project. Which of these mutually exclusive projects do you prefer and why?
Solution: Project X

Square of
NPV × NPV-Arithmetic Square of
NPV Probability deviation ×
Probability mean deviation
Probability
5,000 1,000 –2,250 50,62,500 0.2 10,12,500
7,500 5,250 250 62,500 0.7 43,750
10,000 1.000 2,750 75,62,500 0.1 7,56,250
Mean 7,250 18,12,500

Standard deviation = 18,12,500  1,346

Project Y
NPV x NPV Square of
NPV Square of
Probability Arithmetic Probability deviation x
( ) deviation
( ) mean Probability
0 0 – 8,250 680,62,500 0.1 68,06,250
7,500 5,250 –750 5,62,500 0.7 3,93,750
15,000 3.000 6,750 455,62,500 0.2 91.12.500
8,250
Mean 163,12,500

198 LOVELY PROFESSIONAL UNIVERSITY