Page 189 - DMGT404 RESEARCH_METHODOLOGY

Unit 9: Correlation and Regression

Solution: Notes
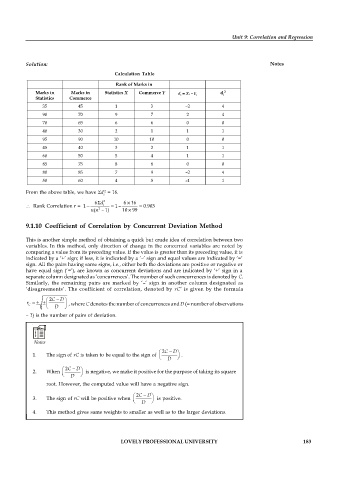
Calculation Table
Rank of Marks in
Marks in Marks in Statistics X Commerce Y i d = X i – Y i d
2
i
Statistics Commerce
35 45 1 3 –2 4
90 70 9 7 2 4
70 65 6 6 0 0
40 30 2 1 1 1
95 90 10 10 0 0
45 40 3 2 1 1
60 50 5 4 1 1
85 75 8 8 0 0
80 85 7 9 –2 4
50 60 4 5 –1 1

2
From the above table, we have d = 16.
i

´
 Rank Correlation r = 1 - 6 d i 2 = 1 – 6 16 = 0.903
´
( n n 2 – 1) 10 99
9.1.10 Coefficient of Correlation by Concurrent Deviation Method
This is another simple method of obtaining a quick but crude idea of correlation between two
variables. In this method, only direction of change in the concerned variables are noted by
comparing a value from its preceding value. If the value is greater than its preceding value, it is
indicated by a ‘+’ sign; if less, it is indicated by a ‘–’ sign and equal values are indicated by ‘=’
sign. All the pairs having same signs, i.e., either both the deviations are positive or negative or
have equal sign (‘=’), are known as concurrent deviations and are indicated by ‘+’ sign in a
separate column designated as ‘concurrences’. The number of such concurrences is denoted by C.
Similarly, the remaining pairs are marked by ‘–’ sign in another column designated as
‘disagreements’. The coefficient of correlation, denoted by rC is given by the formula
C
 2  D 
r C      , where C denotes the number of concurrences and D (= number of observations
 D 
– 1) is the number of pairs of deviation.

Notes
C
 2  D 
1. The sign of rC is taken to be equal to the sign of   .
 D 
C
 2  D 
2. When   is negative, we make it positive for the purpose of taking its square
 D 
root. However, the computed value will have a negative sign.
C
 2  D 
3. The sign of rC will be positive when   is positive.
 D 
4. This method gives same weights to smaller as well as to the larger deviations.

LOVELY PROFESSIONAL UNIVERSITY 183