Page 176 - DCOM504_SECURITY_ANALYSIS_AND_PORTFOLIO_MANAGEMENT

Unit 6: Technical Analysis

6.4 Old Puzzles and New Developments Notes

Fibonacci Numbers
Fibonacci numbers have intrigued mathematicians and scientists for hundred of years. Leonardo
Fionacci (1170-1240) was a medieval mathematician who discovered the series of numbers
while studying the reproductive behaviour of rabbits. The beginning of the Fibonacci series is
shown below: 1,1,2,3,5,8,13,21,34,55,89,144,233,…….
After the initial pair of ones, each succeeding number is simply the sum of the previous two.
The remarkable thing about these numbers is the frequency with which they appear in the
environment. Sunflowers have seeds spiralling around the centre of the plant. Some spirals
contain seeds leaning counter-clockwise, with other spirals going the other way. On most
sunflowers, the number of clockwise and counter-clockwise spirals are adjacent Fibonacci
numbers. A blossom might have 34 counter-clockwise spirals and 55 clockwise spirals. The
structure of pine cones, the number of chambers in a nautilus seashell, the topology of spiralling
galaxies, and the ancestry of bees all reveal Fibonacci numbers. There is even a professional
journal, the Fibonacci Quarterly, which devoted to the study of this series.
1. Technical analysts who follow Fibonacci numbers usually make use of the number 1.613.
This number is called the golden mean and appears in ancient writings and architecture.
(The golden mean features prominently in the dimensions of the Parthenon). After the
first ten or so numbers in the series, each Fibonacci number divided by its immediate
predecessor equals 1.618. For example, 89/55 = 1.618, 134/89 = 1.6189, and so on. This
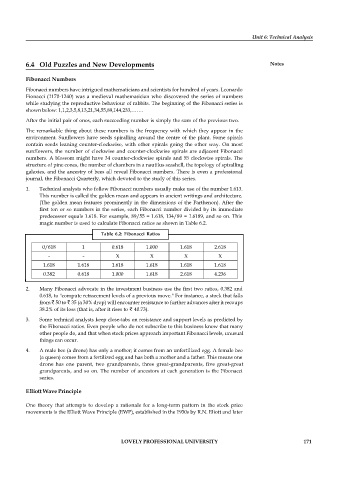
magic number is used to calculate Fibonacci ratios as shown in Table 6.2.

Table 6.2: Fibonacci Ratios

0/618 1 0.618 1.000 1.618 2.618
- - X X X X
1.618 1.618 1.618 1.618 1.618 1.618
0.382 0.618 1.000 1.618 2.618 4.236

2. Many Fibonacci advocate in the investment business use the first two ratios, 0.382 and
0.618, to "compute retracement levels of a previous move." For instance, a stock that falls
from 50 to 35 (a 30% drop) will encounter resistance to further advances after it recoups
38.2% of its loss (that is, after it rises to 40.73).

3. Some technical analysts keep close-tabs on resistance and support levels as predicted by
the Fibonacci ratios. Even people who do not subscribe to this business know that many
other people do, and that when stock prices approach important Fibonacci levels, unusual
things can occur.
4. A male bee (a drone) has only a mother; it comes from an unfertilized egg. A female bee
(a queen) comes from a fertilized egg and has both a mother and a father. This means one
drone has one parent, two grandparents, three great-grandparents, five great-great
grandparents, and so on. The number of ancestors at each generation is the Fibonacci
series.

Elliott Wave Principle

One theory that attempts to develop a rationale for a long-term pattern in the stock price
movements is the Elliott Wave Principle (EWP), established in the 1930s by R.N. Eliott and later

LOVELY PROFESSIONAL UNIVERSITY 171