Page 305 - DCOM504_SECURITY_ANALYSIS_AND_PORTFOLIO_MANAGEMENT

Security Analysis and Portfolio Management

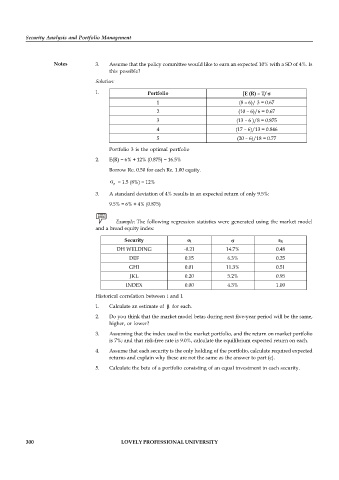
Notes 3. Assume that the policy committee would like to earn an expected 10% with a SD of 4%. Is
this possible?
Solution:

1. Portfolio [E (R) – T/
1 (8 – 6)/ 3 = 0.67
2 (10 – 6)/6 = 0.67
3 (13 – 6 )/8 = 0.875
4 (17 – 6)/13 = 0.846
5 (20 – 6)/18 = 0.77

Portfolio 3 is the optimal portfolio
2. E(R) = 6% + 12% (0.875) = 16.5%

Borrow Re. 0.50 for each Re. 1.00 equity.

p = 1.5 (8%) = 12%
3. A standard deviation of 4% results in an expected return of only 9.5%:
9.5% = 6% + 4% (0.875)

Example: The following regression statistics were generated using the market model
and a broad equity index:
Security σ i r it
DH WELDING -0.21 14.7% 0.48
DEF 0.15 6.3% 0.25
GHI 0.01 11.3% 0.51
JKL 0.20 5.2% 0.95
INDEX 0.00 4.3% 1.00

Historical correlation between i and l.
1. Calculate an estimate of for each.
2. Do you think that the market model betas during next five-year period will be the same,
higher, or lower?

3. Assuming that the index used in the market portfolio, and the return on market portfolio
is 7%; and that risk-free rate is 9.0%, calculate the equilibrium expected return on each.
4. Assume that each security is the only holding of the portfolio, calculate required expected
returns and explain why these are not the same as the answer to part (c).
5. Calculate the beta of a portfolio consisting of an equal investment in each security.

300 LOVELY PROFESSIONAL UNIVERSITY