Page 308 - DCOM504_SECURITY_ANALYSIS_AND_PORTFOLIO_MANAGEMENT

Unit 12: Models

Notes
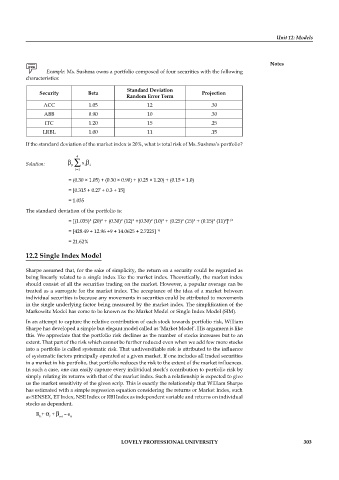
Example: Ms. Sushma owns a portfolio composed of four securities with the following
characteristics:
Standard Deviation
Security Beta Projection
Random Error Term
ACC 1.05 12 .30
ABB 0.90 10 .30
ITC 1.20 15 .25
LRBL 1.00 11 .15

If the standard deviation of the market index is 20%, what is total risk of Ms. Sushma’s portfolio?

4
Solution: p x i i
i 1
= (0.30 × 1.05) + (0.30 × 0.90) + (0.25 × 1.20) + (0.15 × 1.0)
= [0.315 + 0.27 + 0.3 + 15]

= 1.035
The standard deviation of the portfolio is:
2 1/2
2
= [(1.035) (20) + (0.30) (12) +(0.30) (10) + (0.25) (15) + (0.15) (11) ]
2
2
2
2
2
2
2
2
= [428.49 + 12.96 +9 + 14.0625 + 2.7225] ½
= 21.62%
12.2 Single Index Model
Sharpe assumed that, for the sake of simplicity, the return on a security could be regarded as
being linearly related to a single index like the market index. Theoretically, the market index
should consist of all the securities trading on the market. However, a popular average can be
treated as a surrogate for the market index. The acceptance of the idea of a market between
individual securities is because any movements in securities could be attributed to movements
in the single underlying factor being measured by the market index. The simplification of the
Markowitz Model has come to be known as the Market Model or Single Index Model (SIM).
In an attempt to capture the relative contribution of each stock towards portfolio risk, William
Sharpe has developed a simple but elegant model called as ‘Market Model’. His argument is like
this. We appreciate that the portfolio risk declines as the number of stocks increases but to an
extent. That part of the risk which cannot be further reduced even when we add few more stocks
into a portfolio is called systematic risk. That undiversifiable risk is attributed to the influence
of systematic factors principally operated at a given market. If one includes all traded securities
in a market in his portfolio, that portfolio reduces the risk to the extent of the market influences.
In such a case, one can easily capture every individual stock’s contribution to portfolio risk by
simply relating its returns with that of the market index. Such a relationship is expected to give
us the market sensitivity of the given scrip. This is exactly the relationship that William Sharpe
has estimated with a simple regression equation considering the returns or Market Index, such
as SENSEX, ET Index, NSE Index or RBI Index as independent variable and returns on individual
stocks as dependent.
R + + – e
it i mt it

LOVELY PROFESSIONAL UNIVERSITY 303