Page 311 - DCOM504_SECURITY_ANALYSIS_AND_PORTFOLIO_MANAGEMENT

Security Analysis and Portfolio Management

Notes
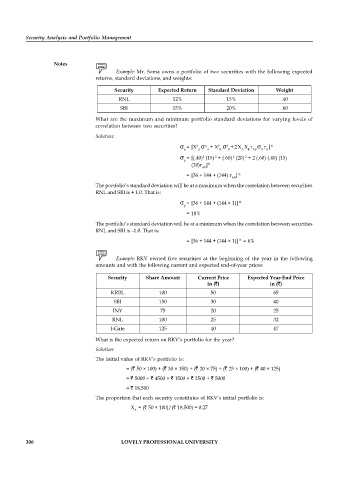
Example: Mr. Soma owns a portfolio of two securities with the following expected
returns, standard deviations, and weights:
Security Expected Return Standard Deviation Weight
RNL 12% 15% .40
SBI 15% 20% .60

What are the maximum and minimum portfolio standard deviations for varying levels of
correlation between two securities?
Solution:

2
= [X 2 A + X 2 + 2 X X r r ] ½
p A A B B A B AB A B
2
= [(.40) (15) + (.60) (20) + 2 (.60) (.40) (15)
2
2
2
p
(20)r ] ½
AB
= [36 + 144 + (144) r ] ½
AB
The portfolio’s standard deviation will be at a maximum when the correlation between securities
RNL and SBI is + 1.0. That is:
= [36 + 144 + (144 × 1)] ½
p
= 18%
The portfolio’s standard deviation will be at a minimum when the correlation between securities
RNL and SBI is –1.0. That is:
= [36 + 144 + (144 × 1)] = 6%
½

Example: RKV owned five securities at the beginning of the year in the following
amounts and with the following current and expected end-of-year prices:
Security Share Amount Current Price Expected Year-End Price
in ( ) in ( )
KRBL 100 50 65
SBI 150 30 40
INY 75 20 25
RNL 100 25 32
I-Gate 125 40 47

What is the expected return on RKV’s portfolio for the year?
Solution:
The initial value of RKV’s portfolio is:
= ( 50 × 100) + ( 30 × 150) + ( 20 × 75) + ( 25 × 100) + ( 40 × 125)
= 5000 + 4500 + 1500 + 2500 + 5000

= 18,500
The proportion that each security constitutes of RKV’s initial portfolio is:
X = ( 50 × 100)/( 18,500) = 0.27
A

306 LOVELY PROFESSIONAL UNIVERSITY