Page 86 - DCOM510_FINANCIAL_DERIVATIVES

Unit 6: Valuation and Pricing of Options

Notes
!
Caution If call or put option prices deviated substantially then, transactions in them
would drive prices up or down until the arbitrage is eliminated.

Below we discuss put-call parity under two different cases i.e., with no dividends and with
dividends.

Put-Call Parity (no Dividends)

The price of a call and a put are linked via the put-call parity relationship. The idea here is that
holding the stock and buying a put is going to deliver the exact same payoffs as buying one call
and investing the present value of the exercise price. Let’s demonstrate this. Consider the payoffs
of two portfolios. Portfolio A contains the stock and a put. Portfolio B contains a call and an
investment of the present value of the exercise price. The value of Portfolio A on expiration date
is shown in Table 6.1 and that of Portfolio B is shown in Table 6.2.

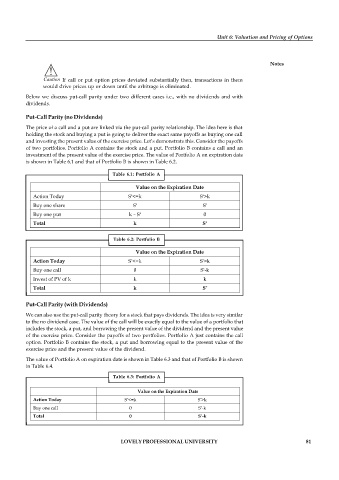
Table 6.1: Portfolio A

Value on the Expiration Date
*
Action Today S <=k S >k
*
*
Buy one share S S
*
Buy one put k – S 0
*
*
Total k S

Table 6.2: Portfolio B
Value on the Expiration Date
*
*
Action Today S <=k S >k
*
Buy one call 0 S -k
Invest of PV of k k k
Total k S
*

Put-Call Parity (with Dividends)

We can also use the put-call parity theory for a stock that pays dividends. The idea is very similar
to the no dividend case. The value of the call will be exactly equal to the value of a portfolio that
includes the stock, a put, and borrowing the present value of the dividend and the present value
of the exercise price. Consider the payoffs of two portfolios. Portfolio A just contains the call
option. Portfolio B contains the stock, a put and borrowing equal to the present value of the
exercise price and the present value of the dividend.
The value of Portfolio A on expiration date is shown in Table 6.3 and that of Portfolio B is shown
in Table 6.4.
Table 6.3: Portfolio A

Value on the Expiration Date
Action Today S <=k S >k
*
*
*
Buy one call 0 S -k
Total 0 S -k
*

LOVELY PROFESSIONAL UNIVERSITY 81