Page 50 - DCAP313_LAB_ON_COMPUTER_GRAPHICS

Lab on Computer Graphics

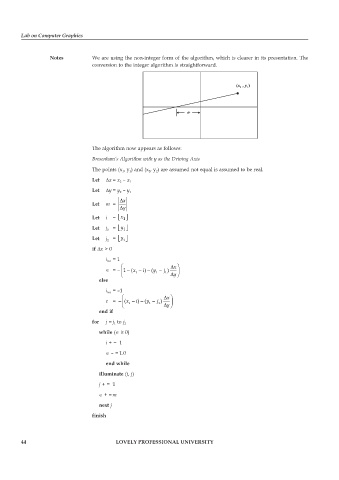
Notes We are using the non-integer form of the algorithm, which is clearer in its presentation. The
conversion to the integer algorithm is straightforward.

The algorithm now appears as follows:
Bresenham’s Algorithm with y as the Driving Axis
The points (x 1 , y 1 ) and (x 2 , y 2 ) are assumed not equal is assumed to be real.

Let ∆x = x 2 – x 1

Let ∆y = y 2 – y 1
Dx
Let m =
Dy
Let i = x Í Î 1 ˙ ˚
Let j 1 = y Í Î 1 ˙ ˚
Let j 2 = y Í Î 2 ˚ ˙

if ∆x > 0
i inc = 1
Ê D x ˆ
 = – 1 - (x 1 - ) (i - y 1 - j 1 ) D y ˜ ¯
Á
Ë
else
i inc = –1
Ê D x ˆ
ε = - (x 1 - ) (y 1 - j 1 ) D y ˜ ¯
i
-
Á
Ë
end if
for j = j 1 to j 2
while ( ≥ 0)
i + = 1

 – = 1.0
end while
illuminate (i, j)

j + = 1
 + = m
next j
finish

44 LOVELY PROFESSIONAL UNIVERSITY