Page 47 - DCAP313_LAB_ON_COMPUTER_GRAPHICS

Unit 3: Implementing Line Algorithm

end if Notes
i + = 1
 + = m
next i
finish
The Integer Bresenham’s Algorithm for Lines with Arbitrary Endpoints
Bresenham’s Algorithm was adapted to lines that have endpoints with arbitrary genuine
coordinates. This algorithm again requires the use of floating point arithmetic to calculate the
slope of the line and to evaluate the error term. We note that is initialized to:
Ê D ( y 1 - (x - Í Î x 1 ˙ ˚ ˆ )
 = – 1 - (y 1 - Íy 1˚ ˙ - D 1 x ˜ ¯
)
Î
Á
Ë
And is incremented by ∆y/∆x at each step. However, we cannot do the same implications with
these algorithms we did with the integer algorithm above, since in this case both ∆y and ∆x
are real ε not integer.
If we multiply through by ∆x, we again obtain an approximation for Œ that, at least, does not
require division.
–
y ˙ +))
 = Dxe= - Dx(1 - ( y - Í Î 1 ˚ Dy(1 - ( x - Í Î 1 ))
x ˙ ˚
1
1
However, to bring this algorithm back to integer form we assume that our basic pixel element
is no longer 1  1 in size, but now it is m  m in size, and utilize increments and decrements
in the algorithm of [m∆x] and [m∆y], respectively. The error term is first set to [ me ] and the
algorithm then proceeds as does the version with endpoints that have integer coordinates. If we
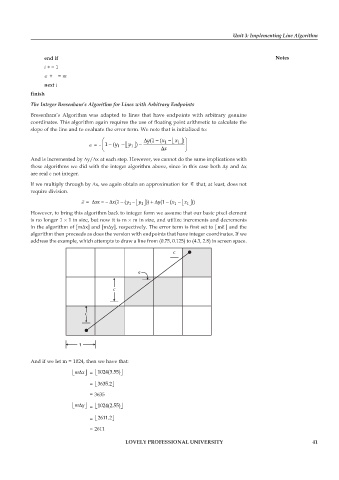
address the example, which attempts to draw a line from (0.75, 0.125) to (4.3, 2.8) in screen space.

And if we let m = 1024, then we have that:

(.
D
Í Î mx˙ ˚ = Í Î 1024 355)˙ ˚
= 3635 2. ˙ ˚
Í Î
= 3635
D
(.
Í Î my˙ ˚ = Î Í 1024 255)˙ ˚
.
= Í Î 2611 2˙ ˚
= 2611

LOVELY PROFESSIONAL UNIVERSITY 41