Page 43 - DCAP313_LAB_ON_COMPUTER_GRAPHICS

Unit 3: Implementing Line Algorithm

end if Notes
i + = 1
 + = m
next i
finish
All algorithms presented in these notes suppose that ∆x and ∆y are positive. If this is not the
case, the algorithm is basically the equal with the exception of the following:
• ε is calculated using |∆y/∆x|.
• x and y are decremented (instead of incremented) by one if the sign of ∆x or ∆y is less
than zero, respectively.
3.2.2 The Integer Bresenham’s Algorithm

Bresenham’s Algorithm, as given, in the previous section, requires the use of floating point
arithmetic to determine the slope of the line and to evaluate the error term. We note that is
initialized to ε = (∆y/∆x) − 1 and is incremented by ∆y/∆x at each step. Since both ∆y and ∆x
are integer quantities, we can convert to an all integer format by multiplying the operations
through by ∆x. That is, we will consider the integer quantity Œ , where Œ is initialized to:
Œ = ∆x ε = ∆y − ∆x

And we will increment Œ by ∆y at each step, and decrement it by ∆x when becomes positive.
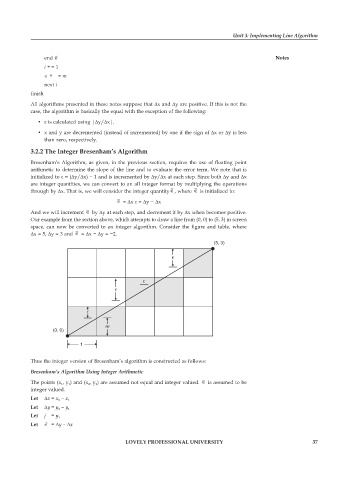
Our example from the section above, which attempts to draw a line from (0, 0) to (5, 3) in screen
space, can now be converted to an integer algorithm. Consider the figure and table, where
∆x = 5, ∆y = 3 and Œ = ∆x − ∆y = −2.

Thus the integer version of Bresenham’s algorithm is constructed as follows:

Bresenham’s Algorithm Using Integer Arithmetic
The points (x 1 , y 1 ) and (x 2 , y 2 ) are assumed not equal and integer valued. Πis assumed to be
integer valued.
Let ∆x = x 2 – x 1
Let ∆y = y 2 – y 1
y
Let j = 1
–
Let  = ∆y – ∆x

LOVELY PROFESSIONAL UNIVERSITY 37