Page 144 - DMTH201_Basic Mathematics-1
P. 144
Unit 5: Equations of Straight Lines
Notes
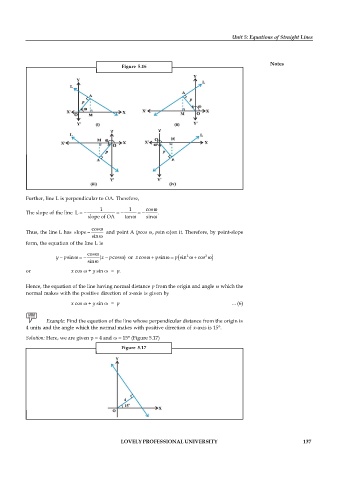
Figure 5.16
Further, line L is perpendicular to OA. Therefore,
1 1 cos
The slope of the line L .
slope of OA tan sin
cos
Thus, the line L has slope and point A (pcos , psin )on it. Therefore, by point-slope
sin
form, the equation of the line L is
cos
x
y p sin (x p cos ) or cos y sin p sin 2 cos 2
sin
or x cos + y sin = p.
Hence, the equation of the line having normal distance p from the origin and angle which the
normal makes with the positive direction of x-axis is given by
x cos + y sin = p ... (6)
Example: Find the equation of the line whose perpendicular distance from the origin is
4 units and the angle which the normal makes with positive direction of x-axis is 15°.
Solution: Here, we are given p = 4 and = 15° (Figure 5.17)
Figure 5.17
LOVELY PROFESSIONAL UNIVERSITY 137