Page 140 - DMTH201_Basic Mathematics-1

Unit 5: Equations of Straight Lines

Notes
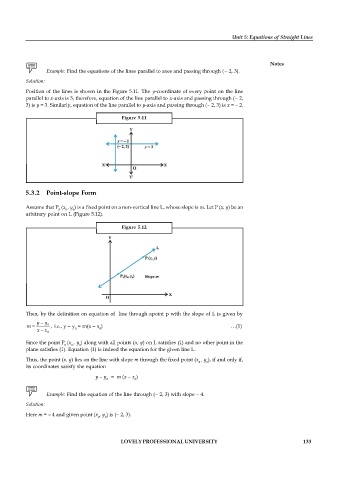
Example: Find the equations of the lines parallel to axes and passing through ( 2, 3).
Solution:

Position of the lines is shown in the Figure 5.11. The y-coordinate of every point on the line
parallel to x-axis is 3, therefore, equation of the line parallel to x-axis and passing through ( 2,
3) is y = 3. Similarly, equation of the line parallel to y-axis and passing through ( 2, 3) is x = 2.
Figure 5.11

5.3.2 Point-slope Form

Assume that P (x , y ) is a fixed point on a non-vertical line L, whose slope is m. Let P (x, y) be an
0 0 0
arbitrary point on L (Figure 5.12).
Figure 5.12

Then, by the definition on equation of line through apoint p with the slope of L is given by
y y
m 0 , i.e., y y = m(x x ) …(1)
x x 0 0 0

Since the point P (x , y ) along with all points (x, y) on L satisfies (1) and no other point in the
0 0 0
plane satisfies (1). Equation (1) is indeed the equation for the given line L.
Thus, the point (x, y) lies on the line with slope m through the fixed point (x , y ), if and only if,
0 0
its coordinates satisfy the equation
y y = m (x x )
0 0

Example: Find the equation of the line through ( 2, 3) with slope 4.
Solution:
Here m = – 4 and given point (x , y ) is ( 2, 3).
0 0

LOVELY PROFESSIONAL UNIVERSITY 133