Page 170 - DMTH201_Basic Mathematics-1

Unit 6: Functions

Notes
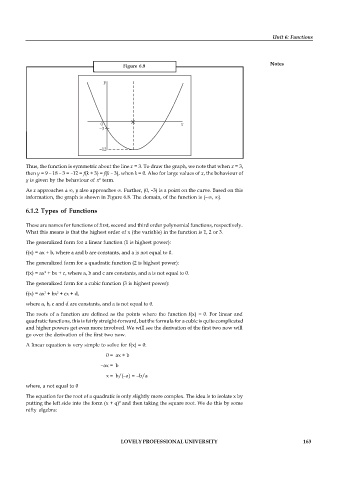
Figure 6.8

0
–3

–12

Thus, the function is symmetric about the line x = 3. To draw the graph, we note that when x = 3,
then y = 9 – 18 – 3 = –12 = f(k + 3) = f(k – 3), when k = 0. Also for large values of x, the behaviour of
2
y is given by the behaviour of x term.
As x approaches ± , y also approaches . Further, (0, –3) is a point on the curve. Based on this
information, the graph is shown in Figure 6.8. The domain, of the function is (– , ).

6.1.2 Types of Functions

These are names for functions of first, second and third order polynomial functions, respectively.
What this means is that the highest order of x (the variable) in the function is 1, 2 or 3.

The generalized form for a linear function (1 is highest power):
f(x) = ax + b, where a and b are constants, and a is not equal to 0.
The generalized form for a quadratic function (2 is highest power):
2
f(x) = ax + bx + c, where a, b and c are constants, and a is not equal to 0.
The generalized form for a cubic function (3 is highest power):
f(x) = ax + bx + cx + d,
3
2
where a, b, c and d are constants, and a is not equal to 0.
The roots of a function are defined as the points where the function f(x) = 0. For linear and
quadratic functions, this is fairly straight-forward, but the formula for a cubic is quite complicated
and higher powers get even more involved. We will see the derivation of the first two now will
go over the derivation of the first two now.
A linear equation is very simple to solve for f(x) = 0:
0 = ax + b

ax = b
x = b/( a) = b/a
where, a not equal to 0
The equation for the root of a quadratic is only slightly more complex. The idea is to isolate x by
putting the left side into the form (x + q) and then taking the square root. We do this by some
2
nifty algebra:

LOVELY PROFESSIONAL UNIVERSITY 163