Page 193 - DMTH202_BASIC_MATHEMATICS_II

Basic Mathematics-II

Notes The dark bars signify when “Heads” (=1) emerges. We can also scheme the average number of
“Heads” beside the number of tosses. In the same Matlab program, this is performed in two
additional lines of code:
y = cumsum(x)./[1:100]
plot(y)
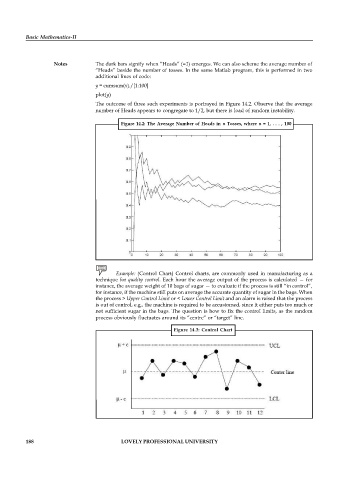
The outcome of three such experiments is portrayed in Figure 14.2. Observe that the average
number of Heads appears to congregate to 1/2, but there is load of random instability.

Figure 14.2: The Average Number of Heads in n Tosses, where n = 1, . . . , 100

Example: (Control Chart) Control charts, are commonly used in manufacturing as a
technique for quality control. Each hour the average output of the process is calculated — for
instance, the average weight of 10 bags of sugar — to evaluate if the process is still “in control”,
for instance, if the machine still puts on average the accurate quantity of sugar in the bags. When
the process > Upper Control Limit or < Lower Control Limit and an alarm is raised that the process
is out of control, e.g., the machine is required to be accustomed, since it either puts too much or
not sufficient sugar in the bags. The question is how to fix the control limits, as the random
process obviously fluctuates around its “centre” or “target” line.

Figure 14.3: Control Chart

188 LOVELY PROFESSIONAL UNIVERSITY