Page 195 - DMTH202_BASIC_MATHEMATICS_II

Basic Mathematics-II

Notes
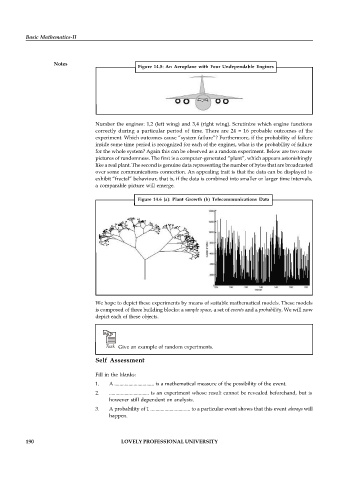
Figure 14.5: An Aeroplane with Four Undependable Engines

Number the engines: 1,2 (left wing) and 3,4 (right wing). Scrutinize which engine functions
correctly during a particular period of time. There are 24 = 16 probable outcomes of the
experiment. Which outcomes cause “system failure”? Furthermore, if the probability of failure
inside some time period is recognized for each of the engines, what is the probability of failure
for the whole system? Again this can be observed as a random experiment. Below are two more
pictures of randomness. The first is a computer-generated “plant”, which appears astonishingly
like a real plant. The second is genuine data representing the number of bytes that are broadcasted
over some communications connection. An appealing trait is that the data can be displayed to
exhibit “fractal” behaviour, that is, if the data is combined into smaller or larger time intervals,
a comparable picture will emerge.

Figure 14.6 (a): Plant Growth (b) Telecommunications Data

We hope to depict these experiments by means of suitable mathematical models. These models
is composed of three building blocks: a sample space, a set of events and a probability. We will now
depict each of these objects.

Task Give an example of random experiments.
Self Assessment

Fill in the blanks:
1. A ............................... is a mathematical measure of the possibility of the event.
2. ............................... is an experiment whose result cannot be revealed beforehand, but is
however still dependent on analysis.
3. A probability of 1 ............................... to a particular event shows that this event always will
happen.

190 LOVELY PROFESSIONAL UNIVERSITY