Page 17 - DMTH201_Basic Mathematics-1

Basic Mathematics – I

Notes 1.4 Inverse Trigonometric Functions

1.4.1 The Arcsine Function

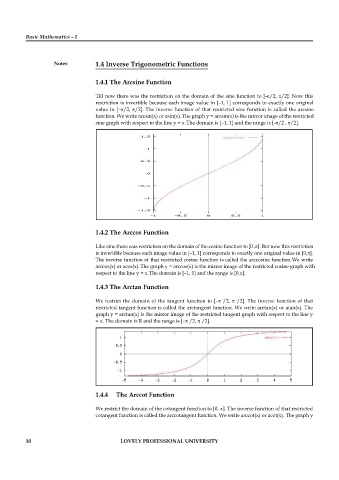
Till now there was the restriction on the domain of the sine function to [– /2, /2]. Now this
restriction is invertible because each image value in [–1, 1] corresponds to exactly one original
value in [– /2, /2]. The inverse function of that restricted sine function is called the arcsine
function. We write arcsin(x) or asin(x). The graph y = arcsin(x) is the mirror image of the restricted
sine graph with respect to the line y = x.The domain is [–1, 1] and the range is [– /2 , /2].

1.4.2 The Arccos Function

Like sine there was restriction on the domain of the cosine function to [0 , ]. But now this restriction
is invertible because each image value in [–1, 1] corresponds to exactly one original value in [0, ].
The inverse function of that restricted cosine function is called the arccosine function.We write
arccos(x) or acos(x). The graph y = arccos(x) is the mirror image of the restricted cosine graph with
respect to the line y = x.The domain is [–1, 1] and the range is [0, ].

1.4.3 The Arctan Function

We restrict the domain of the tangent function to [– /2, /2]. The inverse function of that
restricted tangent function is called the arctangent function. We write arctan(x) or atan(x). The
graph y = arctan(x) is the mirror image of the restricted tangent graph with respect to the line y
= x. The domain is R and the range is [– /2, /2].

1.4.4 The Arccot Function

We restrict the domain of the cotangent function to [0, ]. The inverse function of that restricted
cotangent function is called the arccotangent function. We write arccot(x) or acot(x). The graph y

10 LOVELY PROFESSIONAL UNIVERSITY