Page 57 - DCAP504_Computer Graphics

Computer Graphics

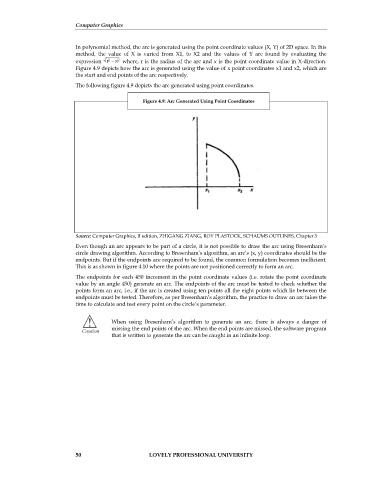
In polynomial method, the arc is generated using the point coordinate values (X, Y) of 2D space. In this
method, the value of X is varied from X1, to X2 and the values of Y are found by evaluating the
expression where, r is the radius of the arc and x is the point coordinate value in X-direction.
Figure 4.9 depicts how the arc is generated using the value of x point coordinates x1 and x2, which are
the start and end points of the arc respectively.
The following figure 4.9 depicts the arc generated using point coordinates.
Figure 4.9: Arc Generated Using Point Coordinates

Source: Computer Graphics, II edition, ZHIGANG ZIANG, ROY PLASTOCK, SCHAUMS OUTLINES, Chapter 3
Even though an arc appears to be part of a circle, it is not possible to draw the arc using Bresenham’s
circle drawing algorithm. According to Bresenham’s algorithm, an arc’s (x, y) coordinates should be the
endpoints. But if the endpoints are required to be found, the common formulation becomes inefficient.
This is as shown in figure 4.10 where the points are not positioned correctly to form an arc.
The endpoints for each 450 increment in the point coordinate values (i.e. rotate the point coordinate
value by an angle 450) generate an arc. The endpoints of the arc must be tested to check whether the
points form an arc, i.e., if the arc is created using ten points all the eight points which lie between the
endpoints must be tested. Therefore, as per Bresenham’s algorithm, the practice to draw an arc takes the
time to calculate and test every point on the circle’s parameter.

When using Bresenham’s algorithm to generate an arc, there is always a danger of
missing the end points of the arc. When the end points are missed, the software program

that is written to generate the arc can be caught in an infinite loop.

50 LOVELY PROFESSIONAL UNIVERSITY