Page 105 - DCAP605_ADVANCED_DATA_STRUCTURE_AND_ALGORITHMS

Advanced Data Structure and Algorithms

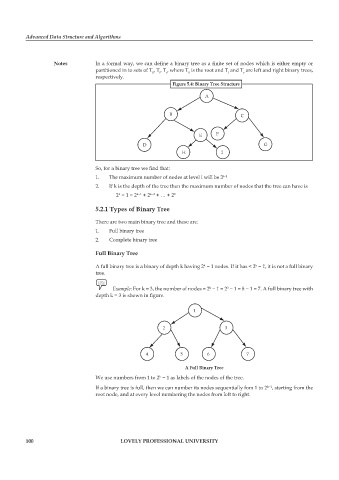
Notes In a formal way, we can define a binary tree as a finite set of nodes which is either empty or
partitioned in to sets of T , T , T , where T is the root and T and T are left and right binary trees,
0
r
r
0
l
l
respectively.
Figure 5.4: Binary Tree Structure
A
B C

E F
D G
H I

So, for a binary tree we fi nd that:
1. The maximum number of nodes at level i will be 2 i−1
2. If k is the depth of the tree then the maximum number of nodes that the tree can have is
k−2
k−1
k
2 − 1 = 2 + 2 + … + 2 0
5.2.1 Types of Binary Tree
There are two main binary tree and these are:
1. Full binary tree
2. Complete binary tree

Full Binary Tree

k
k
A full binary tree is a binary of depth k having 2 − 1 nodes. If it has < 2 − 1, it is not a full binary
tree.
3
k
Example: For k = 3, the number of nodes = 2 − 1 = 2 − 1 = 8 − 1 = 7. A full binary tree with
depth k = 3 is shown in fi gure.
1

2 3

4 5 6 7

A Full Binary Tree
k
We use numbers from 1 to 2 − 1 as labels of the nodes of the tree.
k−1
If a binary tree is full, then we can number its nodes sequentially fom 1 to 2 , starting from the
root node, and at every level numbering the nodes from left to right.

100 LOVELY PROFESSIONAL UNIVERSITY