Page 107 - DCAP605_ADVANCED_DATA_STRUCTURE_AND_ALGORITHMS

Advanced Data Structure and Algorithms

Notes
1 A 1 A
2 B
2 B
3 C 3 C
4 D
5 E
4 D 5 5 E
Array Tree

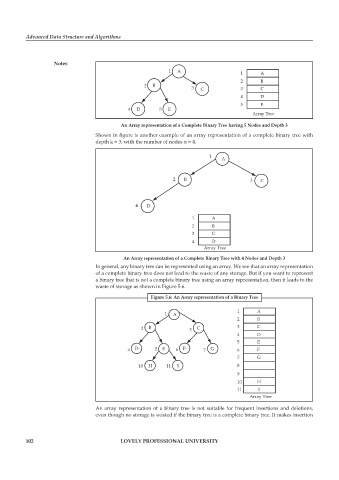
An Array representation of a Complete Binary Tree having 5 Nodes and Depth 3

Shown in figure is another example of an array representation of a complete binary tree with
depth k = 3, with the number of nodes n = 4.

1
A

2 B 3 C

4 D

1 A
2 B
3 C
4 D
Array Tree
An Array representation of a Complete Binary Tree with 4 Nodes and Depth 3
In general, any binary tree can be represented using an array. We see that an array representation
of a complete binary tree does not lead to the waste of any storage. But if you want to represent
a binary tree that is not a complete binary tree using an array representation, then it leads to the
waste of storage as shown in Figure 5.6.
Figure 5.6: An Array representation of a Binary Tree

1 A
1 A
2 B
2 B 3 C 3 C
4 D
5 E
4 D 5 E 6 F 7 G 6 F
7 G
10 H 11 I 8
9
10 H H
11 I
Array Tree

An array representation of a binary tree is not suitable for frequent insertions and deletions,
even though no storage is wasted if the binary tree is a complete binary tree. It makes insertion

102 LOVELY PROFESSIONAL UNIVERSITY