Page 148 - DCAP605_ADVANCED_DATA_STRUCTURE_AND_ALGORITHMS

Unit 6: Binary Search Tree and AVL Trees

Notes
h-1
D

h-2
h-2
B F

h-3

A C E G
h-3 or h-4 h-3 or h-4
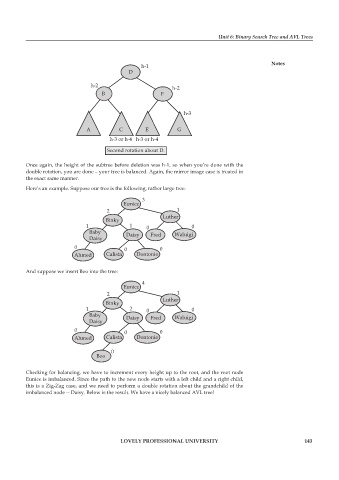
Second rotation about D.

Once again, the height of the subtree before deletion was h-1, so when you’re done with the
double rotation, you are done – your tree is balanced. Again, the mirror image case is treated in
the exact same manner.

Here’s an example. Suppose our tree is the following, rather large tree:
3
Eunice
2 1
Luther
Binky
1 1 0 0
Baby Daisy Fred Waluigi
Daisy
0 0 0
Ahmed Calista Dontonio

And suppose we insert Boo into the tree:
4
Eunice
2 1
Luther
Binky
1 2 0 0
Baby Daisy Fred Waluigi
Daisy
0 0 0
Ahmed Calista Dontonio

0
Boo

Checking for balancing, we have to increment every height up to the root, and the root node
Eunice is imbalanced. Since the path to the new node starts with a left child and a right child,
this is a Zig-Zag case, and we need to perform a double rotation about the grandchild of the
imbalanced node -- Daisy. Below is the result. We have a nicely balanced AVL tree!

LOVELY PROFESSIONAL UNIVERSITY 143