Page 150 - DCAP605_ADVANCED_DATA_STRUCTURE_AND_ALGORITHMS

Unit 6: Binary Search Tree and AVL Trees

The imbalanced node is B. If the height of subtree C is h-3, then the height of E will be h-2 and the Notes
tree is a Zig-Zig – you can rebalance by rotating about node D. If the height of subtree E is h-3,
then the height of C is h-2 and the tree is a Zig-Zag – you rebalance by doing a double rotation
about the root of C. If both C and E have heights of h-2, then you treat it as either a Zig-Zig or a
Zig-Zag. Both work. For the purposes of your lab, treat this case like a Zig-Zig.
The mirror image works the same way.

Let’s look at some examples. First, suppose we delete Calista from the following tree:
2
Binky
1 0
Baby Calista
Daisy
0
Ahmed

You’re left with: 2
Binky
1
Baby
Daisy
0
Ahmed
You check Calista’s old parent – Binky and although Binky’s height hasn’t changed, the node
is imbalanced. It’s clearly a Zig-Zig tree, so you rotate about Baby Daisy to yield the following
tree:

1
Baby
Daisy
0 0
Ahmed Binky

Since Baby Daisy is the root, we’re done.
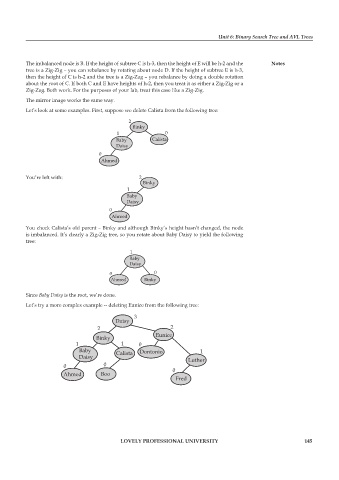
Let’s try a more complex example -- deleting Eunice from the following tree:

3
Daisy
2 2
Eunice
Binky
1 1 0
Baby Calista Dontonio 1
Daisy Luther
0 0
Ahmed Boo 0
Fred

LOVELY PROFESSIONAL UNIVERSITY 145